题目内容
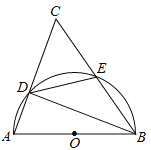
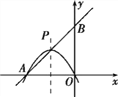
【题目】如图所示,直线y=![]() +3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-
+3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-![]() x2+bx+c经过点A,P,O(原点).
x2+bx+c经过点A,P,O(原点).
(1)求抛物线的表达式;
(2)在x轴上方的抛物线上是否存在一点Q,使∠QAO=45°?如果存在,求出Q点的坐标;如果不存在,请说明理由.
【答案】(1)抛物线的表达式为y=-![]() x2-
x2-![]() x;(2)存在,Q点的坐标为
x;(2)存在,Q点的坐标为![]() .
.
【解析】(1)根据直线AB的解析式,可求得B点坐标,而P为线段AB的中点,那么点P的纵坐标为B点纵坐标的一半,由于抛物线经过原点,那么c=0,根据公式法表示出P点纵坐标,即可求得b的值,由此确定该抛物线的解析式.(2)此题应分两种情况讨论:①当Q点在x轴上方时,由于∠OAQ=45°,那么直线AQ的斜率为k=1,而A点坐标易求得,即可得到直线AQ的解析式,联立抛物线的解析式,即可求得Q点坐标;
②当Q点在x轴下方时,方法同①.
(1)直线y=![]() +3与x轴、y轴分别交于点A,B,且P为线段AB的中点,抛物线y=-
+3与x轴、y轴分别交于点A,B,且P为线段AB的中点,抛物线y=-![]() x2+bx+c过A,P,O三点,
x2+bx+c过A,P,O三点,
∴OB=3,c=0,P必为抛物线的顶点,
∴![]() =
=![]() ,∴b=±
,∴b=±![]() .
.
又∵x=-![]() =
=![]() <0,∴b<0,∴b=-
<0,∴b<0,∴b=-![]() .
.
∴抛物线的表达式为y=-![]() x2-
x2-![]() x.
x.
(2)存在.
∵抛物线y=-![]() x2-
x2-![]() x经过点A,
x经过点A,
∴A点的坐标为(-4,0).
设Q点的坐标为(x,y),∵∠QAO=45°,
∴x=-4+y.
将其代入抛物线的关系式中得y=-![]() (-4+y)2-
(-4+y)2-![]() (-4+y),解得y1=0(舍去),y2=
(-4+y),解得y1=0(舍去),y2=![]() .
.
当y=![]() 时,x=-
时,x=-![]() .
.
∴Q点的坐标为![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案【题目】为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计算:当用水量不超过![]() 吨时,每吨的收费标准相同,当用水量超过
吨时,每吨的收费标准相同,当用水量超过![]() 吨时,超出
吨时,超出![]() 吨的部分每吨的收费标准也相同,下表是小明家
吨的部分每吨的收费标准也相同,下表是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
用水量(吨) |
|
|
|
|
费用(元) |
|
|
|
|
请根据表格中提供的信息,回答以下问题:
(1)若小明家![]() 月份用水量为
月份用水量为![]() 吨,则应缴水费________元;
吨,则应缴水费________元;
(2)若某户某月用了![]() 吨水(
吨水(![]() ),应付水费________元;
),应付水费________元;
(3)若小明家![]() 月份交纳水费
月份交纳水费![]() 元,则小明家
元,则小明家![]() 月份用水多少吨?
月份用水多少吨?