题目内容
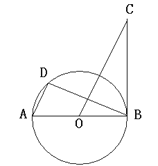
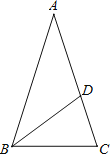
【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由等腰三角形ABC中,顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;
(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;
(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.
试题解析:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∵∠CBD=∠A=36°,∠C=∠C,
∴△ABC∽△BCD;
(2)∵∠A=∠ABD=36°,
∴AD=BD,
∵BD=BC,
∴AD=BD=CD=1,
设CD=x,则有AB=AC=x+1,
∵△ABC∽△BCD,
∴![]() ,即
,即![]() ,
,
整理得:x2+x-1=0,
解得:x1=![]() ,x2=
,x2=![]() (负值,舍去),
(负值,舍去),
则x=![]() ;
;
(3)过B作BE⊥AC,交AC于点E,
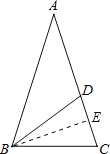
∵BD=CD,
∴E为CD中点,即DE=CE=![]() ,
,
在Rt△ABE中,cosA=cos36°=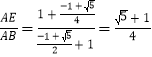 ,
,
在Rt△BCE中,cosC=cos72°=![]() ,
,
则cos36°-cos72°=![]() -
-![]() =
=![]() .
.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
月用水量(吨) | 单价(元/吨) |
不超过25吨 | 1.4 |
超过25吨的部分 | 2.1 |
另:每吨用水加收0.95元的城市污水处理费 | |
(1)如果1月份小明家用水量为18吨,那么小明家1月份应该缴纳水费 元;
(2)小明家2月份共缴纳水费104.5元,那么小明家2月份用水多少吨?
(3)小明家的水表3月份出了故障,只有80%的用水量记入水表中,这样小明家在3月份只缴纳了56.4元水费,问小明家3月份实际应该缴纳水费多少元?