Question

阅读理解题：
【几何模型】
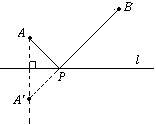
条件：如图1，A、B是直线l同旁的两个定点．
问题：在直线l上确定一点P，使PA+PB的值最小．
方法：作点A关于直线l的对称点A′，连接A′B交l于点P，则PA+PB=A′P+PB=A′B，
由“两点之间，线段最短”可知，点P即为所求的点．

【模型应用】
如图2所示，两个村子A、B在一条河CD的同侧，A、B两村到河边的距离分别为AC=1千米，BD=3千米，CD=3千米．现要在河边CD上建造一水厂，向A、B两村送水，铺设水管的工程费用为每千米15000元，请你在CD上选择水厂位置，使铺设水管的费用最省，并求出最省的铺设水管的费用W．

Answer 1

分析：由于铺设水管的工程费用为每千米15000元，是一个定值，现在要在CD上选择水厂位置，使铺设水管的费用最省，意思是在CD上找一点P，使AP与BP的和最小，设A′是A的对称点，使AP+BP最短就是使A′P+BP最短．

解答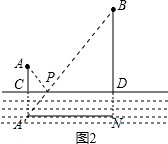：解：解：如图所示：延长AC到点A′，使CA′=AC；连接BA′交CD于点P，
点P就是所选择的位置．
在直角三角形BA′N中，
BN=3+1=4，A′N=3，
∴A′B=

BN2+A′N2

=

32+42

=5（千米），
∴最短路线AP+BP=A′B=5（km），
最省的铺设管道的费用为
W=5×15000=75000（元）
答：最省的铺设管道的费用是75000元．

点评：此题主要考查了最短路径问题，解这类问题的关键是将实际问题抽象或转化为几何模型，把两条线段的和转化为一条线段，运用三角形三边关系解决．