题目内容
【题目】已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形. 
【答案】解:∵AB=AC,
∴∠B=∠C(等边对等角).
∵DE⊥BC于E,
∴∠FEB=∠FEC=90°,
∴∠B+∠EDB=∠C+∠EFC=90°,
∴∠EFC=∠EDB(等角的余角相等).
∵∠EDB=∠ADF(对顶角相等),
∴∠EFC=∠ADF.
∴△ADF是等腰三角形
【解析】先根据等腰三角形的性质得出∠B=∠C,再由等角的余角相等得出∠EFC=∠EDB,进而可得出∠EFC=∠ADF,由此可得出结论.
【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.

练习册系列答案
相关题目
【题目】下面的图形是由边长为1的正方形按照某种规律排列而组成的.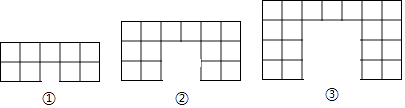
(1)观察图形,填写下表:
图形个数(n) | ① | ② | ③ |
正方形的个数 | 9 | ||
图形的周长 | 16 |
(2)推测第n个图形中,正方形的个数为 , 周长为(都用含n的代数式表示).
(3)写出第2016个图形的周长.

