题目内容
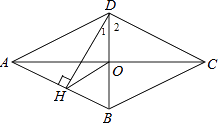
【题目】如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH, 
(1)求证:∠DHO=∠DCO.
(2)若OC=4,BD=6,求菱形ABCD的周长和面积.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠1=∠DHO,
∵DH⊥CD,
∴∠1+∠2=90°,
∵BD⊥AC,
∴∠2+∠DCO=90°,
∴∠1=∠DCO,
∴∠DHO=∠DCO
(2)解:∵四边形ABCD是菱形,
∴OD=OB= ![]() BD=3,OA=OC=4,BD⊥AC,
BD=3,OA=OC=4,BD⊥AC,
在Rt△OCD中,CD= ![]() =5,
=5,
∴菱形ABCD的周长=4CD=20,
菱形ABCD的面积= ![]() ×6×8=24.
×6×8=24.
【解析】(1)先根据菱形的性质得OD=OB,AB∥CD,BD⊥AC,则利用DH⊥AB得到DH⊥CD,∠DHB=90°,所以OH为Rt△DHB的斜边DB上的中线,得到OH=OD=OB,利用等腰三角形的性质得∠1=∠DHO,然后利用等角的余角相等证明结论;(2)先根据菱形的性质得OD=OB= ![]() BD=3,OA=OC=4,BD⊥AC,再根据勾股定理计算出CD,然后利用菱形的性质和面积公式求菱形ABCD的周长和面积.
BD=3,OA=OC=4,BD⊥AC,再根据勾股定理计算出CD,然后利用菱形的性质和面积公式求菱形ABCD的周长和面积.
【考点精析】掌握菱形的性质是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目