题目内容
【题目】如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由. 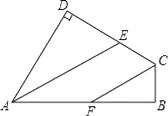
【答案】解:AE∥CF. 理由如下:∵∠B=∠D=90°,
∴∠BAD+∠BCD=360°﹣90°×2=180°,
∵AE、CF分别平分∠BAD和∠BCD,
∴∠1= ![]() ∠BAD,∠2=
∠BAD,∠2= ![]() ∠BCD,
∠BCD,
∴∠1+∠2= ![]() (∠BAD+∠BCD)=
(∠BAD+∠BCD)= ![]() ×180°=90°,
×180°=90°,
∵∠B=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∴AE∥CF.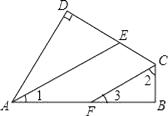
【解析】根据四边形的内角和等于360°求出∠BAD+∠BCD=180°,再根据角平分线的定义求出∠1+∠2=90°,根据直角三角形两锐角互余求出∠2+∠3=90°从而得到∠1=∠3,然后根据同位角相等,两直线平行证明即可.
【考点精析】通过灵活运用平行线的判定,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行即可以解答此题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目