题目内容
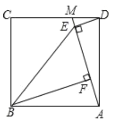
【题目】如图，点M是正方形ABCD边CD上一点，连接AM，作DE⊥AM于点E，作BF⊥AM于点F，连接BE. 若AF=1，四边形ABED的面积为6，则BF的长为（ ）
A.2B.3C.
D.
【答案】B
【解析】
先证明ΔABF≌ΔDAE得到BF=AE，设BF=x，则AE=x，DE=AF=1，利用四边形ABED的面积=
得
，解之即可求得BF的长.
∵四边形ABCD是正方形，
∴BA=AD，∠BAD=90，
∴∠DAE+∠BAF=90，
∵BF⊥AM，DE⊥AM，
∴∠AFB=∠DEA=90，
∴∠ABF+∠BAF=90，
∴∠ABF=∠DAE，
在ΔABF和ΔDAE中
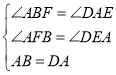
∴ΔABF≌ΔDAE(AAS)，
∴BF=AE，DE=AF=1
设BF=x，则AF=x，
由四边形ABED的面积为6得：
，即，
解得：
（舍去），
∴BF=3，
故选：B.
练习册系列答案
相关题目
