题目内容
【题目】已知射线![]() 平行于射线
平行于射线![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上.
上.

(1)如图1,若点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() 时,则
时,则![]() _________.
_________.
(2)如图1,若点![]() 在线段
在线段![]() 上运动(不包含
上运动(不包含![]() 、
、![]() 两点),则
两点),则![]() 、
、![]() 、
、![]() 之间的等量关系是_____________________.
之间的等量关系是_____________________.
(3)①如图2,若点![]() 在线段
在线段![]() 的延长线上运动,则
的延长线上运动,则![]() 、
、![]() 、
、![]() 之间的等量关系是________________;
之间的等量关系是________________;
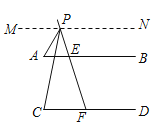
②如图3,若点![]() 在线段
在线段![]() 的延长线上运动,则
的延长线上运动,则![]() 、
、![]() 、
、![]() 之间的等量关系是________________.
之间的等量关系是________________.
(4)请说明图2中所得结论的理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() ;(4)见解析;
;(4)见解析;
【解析】
(1)过P作GH∥CD,根据平行线的性质得∠HPC=∠C,由AB∥CD得到AB∥GH,得到∠APH=∠A,则∠APC=∠HPC+∠APH=∠A+∠C,把∠A=25°,∠APC=70°代入计算可得到∠C的度数;
(2)过P作GH∥CD,根据平行线的性质得∠HPC=∠C,由AB∥CD得到AB∥GH,得到∠APH=∠A,则∠APC=∠HPC+∠APH=∠A+∠C,可得到∠APC=∠A+∠C;
(3)过P作MN∥CD,根据平行线的性质得∠MPC=∠C,由AB∥CD得到AB∥MN,得到∠APM=∠A,则∠APC=∠MPC-∠APM=∠C-∠A,可得到∠APC=∠C-∠A;
② 过P作IJ∥CD,根据平行线的性质得∠IPC=∠C,由AB∥CD得到AB∥IJ,得到∠API=∠A,则∠APC=∠API-∠IPC=∠A-∠C,可得到∠APC=∠A-∠C;
(4)过点![]() 作
作![]() ,由两直线平行,内错角相等,得到
,由两直线平行,内错角相等,得到![]() ,
,![]() ,再由角的关系进行相减即可.
,再由角的关系进行相减即可.
解:
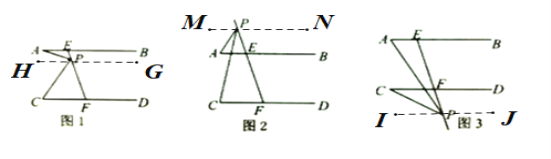
(1)如图1,过P作GH∥CD,
∴∠C=∠CPH.
∵AB∥CD,
∴AB∥GH,
∴∠A=∠APH.
∵∠APC=∠HPC+∠APH=∠A+∠C,
∴∠C=∠APC-∠A=70°-25°=45°.
(2)如图1,如图1,过P作GH∥CD,
∴∠C=∠CPH.
∵AB∥CD,
∴AB∥GH,
∴∠A=∠APH.
∵∠APC=∠HPC+∠APH=∠A+∠C,
∴![]() .
.
(3)①如图2,过P作MN∥CD,
∴∠MPC=∠C.
∵AB∥CD,
∴AB∥MN,
∴∠APM=∠A.
∵∠APC=∠MPC-∠APM=∠C-∠A
∴![]() ;
;
②如图3,过P作IJ∥CD,
∴∠IPC=∠C.
∵AB∥CD,
∴AB∥IJ,
∴∠API=∠A.
∵∠APC=∠API-∠IPC=∠A-∠C
∴![]() .
.
(4)理由:过点![]() 作
作![]()
∵![]()
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()

 阅读快车系列答案
阅读快车系列答案【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<50 | a |
B | 50≤x<100 | 10 |
C | 100≤x<150 | |
D | 150≤x<200 | |
E | x≥200 |
请结合以上信息解答下列问题.

(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?