题目内容
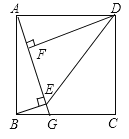
【题目】如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．
（1）求证：△ABE≌△DAF；
（2）若AF=1，S△ADE=8，求EF的长．
【答案】（1）见解析；（2）3
【解析】分析：（1）由∠BAE+∠DAF=90°，∠DAF+∠ADF=90°，推出∠BAE=∠ADF，即可根据AAS证明△ABE≌△DAF；
（2）设EF=x，则AE=DF=x+1，根据S△ADE=8，列出方程即可解决问题．
详解：（1）∵四边形ABCD是正方形，∴AB=AD．
∵DF⊥AG，BE⊥AG，∴∠BAE+∠DAF=90°，∠DAF+∠ADF=90°，∴∠BAE=∠ADF．在△ABE和△DAF中，∵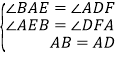
，∴△ABE≌△DAF（AAS）．
（2）设EF=x，则AE=DF=x+1．
由S△ADE=8，得：
（x+1）2=8，
解得：x=3或﹣5（舍弃），∴EF=3．
练习册系列答案
导学教程高中新课标系列答案
相关题目
