Question

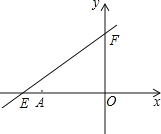
【题目】已知两点，，且点B在第一象限，AB∥x轴，点在y轴上。

（1）求点P的坐标。

（2）试确定的取值范围。

（3）当时，求△PAB的面积S

Answer 1

【答案】（1）P（0，2）．（2）m+n＞4．（3）5.

【解析】

（1）根据点在y轴上横坐标为0，构建方程求出a即可解问题．

（2）根据AB∥x轴，确定m=4，点B在第一象限，确定n＞0，即可解决问题．

（3）根据A，B，C的坐标，画出△ABC，利用三角形面积公式计算即可．

（1）∵点P（a-1，a+1）在y轴上，

∴a-1=0，

∴a=1，

∴P（0，2）．

（2）∵A（-3，m），B（n，4），AB∥x轴，

∴m=4，

∵点B在第一象限，

∴n＞0，

∴m+n＞4．

（3）由题意：A（-3，4），B（2，4），P（0，2），如图，

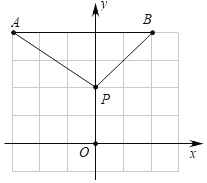
∴S=×5×2=5．