题目内容
【题目】如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( ) 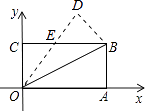
A.(4,8)
B.(5,8)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
【答案】C
【解析】解:∵矩形ABCO中,OA=8,OC=4,
∴BC=OA=8,AB=OC=4,
由折叠得到OD=OA=BC,∠AOB=∠DOB,∠ODB=∠BAO=90°,
在Rt△CBO和Rt△DOB中,![]() ,
,
∴Rt△CBO≌Rt△DOB(HL),
∴∠CBO=∠DOB,
∴OE=EB,
设CE=x,则EB=OE=8﹣x,
在Rt△COE中,根据勾股定理得:(8﹣x)2=x2+42 ,
解得:x=3,
∴CE=3,OE=5,DE=3,
过D作DF⊥BC,可得△COE∽△FDE,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
解得:DF= ![]() ,EF=
,EF= ![]() ,
,
∴DF+OC= ![]() +4=
+4= ![]() ,CF=3+
,CF=3+ ![]() =
= ![]() ,
,
则D( ![]() ,
, ![]() ),
),
故选C.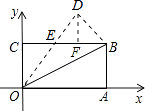
【考点精析】通过灵活运用翻折变换(折叠问题),掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目