Question

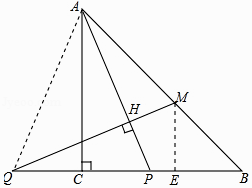
【题目】在等腰直角△ABC中，∠ACB=90°，P是线段BC上一动点（与点B、C不重合），连接AP，延长BC至点Q，使得CQ=CP，过点Q作QH⊥AP于点H，交AB于点M．
（1）若∠PAC=α，求∠AMQ的大小（用含α的式子表示）．
（2）用等式表示线段MB与PQ之间的数量关系，并证明．

Answer 1

【答案】
（1）解：∠AMQ=45°+α；理由如下：

∵∠PAC=α，△ACB是等腰直角三角形，

∴∠BAC=∠B=45°，∠PAB=45°﹣α，

∵QH⊥AP，

∴∠AHM=90°，

∴∠AMQ=180°﹣∠AHM﹣∠PAB=45°+α

（2）解：PQ= MB；理由如下：

连接AQ，作ME⊥QB，如图所示：

∵AC⊥QP，CQ=CP，

∴∠QAC=∠PAC=α，

∴∠QAM=45°+α=∠AMQ，

∴AP=AQ=QM，

在△APC和△QME中， ，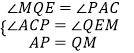

∴△APC≌△QME（AAS），

∴PC=ME，

∴△AEB是等腰直角三角形，

∴ PQ= MB，

∴PQ= MB．

【解析】（1）由等腰直角三角形的性质得出∠BAC=∠B=45°，∠PAB=45°﹣α，由直角三角形的性质即可得出结论；（2）连接AQ，作ME⊥QB，由AAS证明△APC≌△QME，得出PC=ME，△AEB是等腰直角三角形，由等腰直角三角形的性质即可得出结论．
【考点精析】根据题目的已知条件，利用等腰直角三角形的相关知识可以得到问题的答案，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°．