题目内容
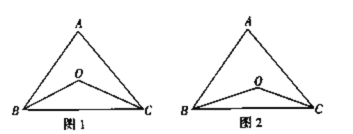
【题目】已知任意一个三角形的三个内角的和是180°，如图1，在ABC中，∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
（1）若∠A=70°，求∠BOC的度数；
（2）若∠A=α，求∠BOC的度数；
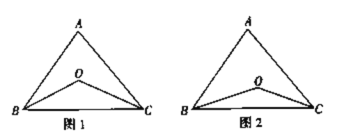
（3）如图2，若BO、CO分别是∠ABC、∠ACB的三等分线，也就是∠OBC=
∠ABC，∠OCB=∠ACB，∠A=α，求∠BOC的度数.
【答案】（1）125°；（2）90°+
；（3）120°+
【解析】
（1）根据三角形的内角和定理求出∠ABC+∠ACB，根据角平分线的定义求出∠OBC+∠OCB，根据三角形内角和定理求出即可；
（2）根据三角形的内角和定理求出∠ABC+∠ACB，根据角平分线的定义求出∠OBC+∠OCB，根据三角形内角和定理求出即可；
（3）根据三角形的内角和定理求出∠ABC+∠ACB，求出∠OBC+∠OCB，根据三角形内角和定理求出即可．
（1）∵∠A=70°，
∴∠ABC+∠ACB=180°-∠A=110°，
∵在△ABC中，∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O，
∴∠OBC=
∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=55°，
∴∠BOC=180°-（∠OBC+∠OCB）=125°；
（2）∵∠A=α，
∴∠ABC+∠ACB=180°-∠A=180°-α，
∵在△ABC中，∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=（180°-α）=90°-α，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-（90°-α）=90°+α；
（3）∵∠A=α，
∴∠ABC+∠ACB=180°-∠A=180°-α，
∵∠OBC=
∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=（180°-α）=60°-α，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-（60°-α）=120°+α．
