��Ŀ����
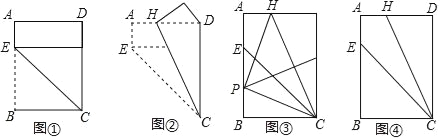
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��a��0������b��0����������![]() ��ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��
��ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��
��1�����C��D�����꼰�ı���ABDC�������
��2����y�����Ƿ����һ��M������MA��MB��ʹS��MAB=S�ı���ABDC������������һ�㣬�����M�����ꣻ�������ڣ���˵�����ɣ�
��3����P������BD�ϵ�һ�����㣨����B��D�غϣ�������PC��PA�����CPA���DCP����BAP֮��Ĺ�ϵ��
���𰸡���1��C(0��2)��D(4��2)��S�ı���ABDC=8����2��M(0��4)��(0��-4)����3����CPA= ��BAP+��DCP���CPA= ��BAP-��DCP��
��������
��1����������ݷǸ������������A��B���꣬���������ó�C��D���꣬�̶���������ı���ABDC�������
��2���������֪��ABΪ�ױߣ����M��AB�ľ���Ϊh��������MAB�ĸߣ����h��ֵ���ɵó���M�����ꣻ
��3����������ֵ���P���߶�BD��ʱ�Լ�����P��BD�ӳ�����ʱ������ƽ���ߵ����ʽ��з�������.
��: ��1����![]() ��a=-1��b=3����A(-1��0)��B(3��0)��
��a=-1��b=3����A(-1��0)��B(3��0)��
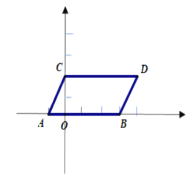
�ߵ�A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D����ͼ��
��C(0��2)��D(4��2)��
��S�ı���ABDC=AB��OC=4��2=8.
��2�����ڣ����M��AB�ľ���Ϊh��S��MAB=![]() ��AB��h=2h��
��AB��h=2h��
��S��MAB=S�ı���ABDC����2h=8�����h=4��
��֪������M����y������������
��M(0��4)��(0��-4).
��3�� �ٵ���P���߶�BD��ʱ����CPA=��DCP+��BAP���������£�
��P����PE��AB��OC��E�㣬
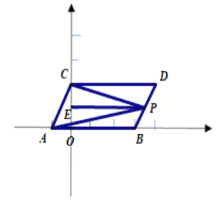
��AB��CD�� PE��AB��
��AB��PE��CD��
���DCP=��CPE�� ��BAP=��APE��
�ߡ�CPA=��CPE+��APE��
���CPA=��DCP+��BAP��
�ڵ���P��BD�ӳ�����ʱ����CPA= ��BAP-��DCP���������£�
��P����PE��AB��

��AB��CD��PE��AB��
��AB��PE��CD��
���DCP=��CPE����BAP=��APE��
�ߡ�CPA= ��APE-��CPE��
���CPA= ��BAP-��DCP.