题目内容
【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5.
①求证:AF⊥BD,
②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时.求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数,若不是,请说明理由.

【答案】(1)AF=![]() (2)见解析(3)∠AFG=45°
(2)见解析(3)∠AFG=45°
【解析】
试题分析:(1)①根据SAS可证△ACE≌△BCD,再根据全等三角形的性质可得∠1=∠2,再结合对顶角相等证得结论;
②根据同一个三角形的面积不变可求的AF得值;
(2)如①的方法,根据SAS证得△ACE≌△BCD,再根据全等三角形的性质和垂直的定义可证;
(3)如图4,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,然后由上面的结论△ACE≌△BCD,可根据全等三角形的面积相等证得CM=CN,再根据角平分线的判定得证CF平分∠BFE,最后根据角平分线的性质得证.
试题解析:(1)①证明:如图1,∵AC=BC,∠ACB=∠ECD=90°,EC=DC,∴△ACE≌△BCD,
∴∠1=∠2,∵∠3=∠4,∴∠BFE=∠ACE=90°,∴AF⊥BD.
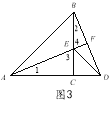
②∵∠ECD=90°,BC= AC=12,DC= EC=5,∴BD=13,
∵S△ABD=![]() AD·BC=
AD·BC=![]() BD·AF,∴AF=
BD·AF,∴AF=![]() .
.
(法2:∵∠ECD=90°,BC= AC=12,DC= EC=5,∴AE=BD=13,BE=7,设EF=x,
∵∠BFE=90°,∴BF2=BE2-EF2,BF2=AB2-AF2,∴72-x2=288-(13+x)2,
∴x=![]() ,∴AF=13+
,∴AF=13+![]() =
=![]() .)
.)
(2)证明:如图4,∵∠ACB=∠ECD,∴∠ACB+∠ACD=∠ECD+∠ACD,∴∠BCD=∠ACE,
∵AC=BC,∠ACE=∠BCD,EC=DC,∴△ACE≌△BCD,∴∠1=∠2,
∵∠3=∠4,∴∠BFA=∠BCA=90°,∴AF⊥BD.
(3)∠AFG=45°.
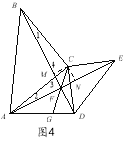
如图4,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,
∵△ACE≌△BCD,∴S△ACE=S△BCD,AE=BD,∵S△ACE=![]() AE·CN,
AE·CN,
S△BCD=![]() BD·CM,∴CM=CN,
BD·CM,∴CM=CN,
∵CM⊥BD,CN⊥AE,∴CF平分∠BFE,
∵AF⊥BD,∴∠BFE=90°,∴∠EFC=45°,∴∠AFG=45°.
(法2:过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,∵CM⊥BD,CN⊥AE,
∴∠BMC=∠ANC=90°,∵△ACE≌△BCD,∴∠1=∠2,∵∠BMC=∠ANC=90°,∠1=∠2,
AC=BC,∴△BCM≌△ACN,∴CM=CN,∵CM⊥BD,CN⊥AE,∴CF平分∠BFE,
∵AF⊥BD,∴∠BFE=90°,∴∠EFC=45°,∴∠AFG=45°.)

 名校课堂系列答案
名校课堂系列答案