题目内容
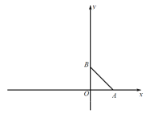
【题目】平面直角坐标系中,点A、B分别在x轴正半轴、y轴正半轴上,AO=BO,△ABO的面积为8.
(1)求点A的坐标;
(2)点C、D分别在x轴负半轴、y轴正半轴上(D在B点上方),AB⊥CD于E,设点D纵坐标为t,△BCE的面积为S,求S与t的函数关系;
(3)在(2)的条件下,点F为BE中点,连接OF交BC于G,当∠FOB+∠DAE=45°时,求点E坐标.


【答案】(1)A(4,0);(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用三角形的面积公式构建方程即可解决问题.
(2)证明△CEA和△COD是等腰直角三角形,由EN⊥AC,推出![]() ,AC=4+t,根据S=S△AEC-S△ABC计算即可.
,AC=4+t,根据S=S△AEC-S△ABC计算即可.
(3)过点F作FM⊥AC于点M,由(2)求出点F的坐标为![]() ,从而得到
,从而得到
![]() ,
,![]() ,由∠ABO=∠BDA+∠BAD=45°,∠FOB+∠DAE=45°,得出∠FOB=∠BDA,进而得出∠MFO=∠ODA,tan∠MFO =tan∠ODA,故而
,由∠ABO=∠BDA+∠BAD=45°,∠FOB+∠DAE=45°,得出∠FOB=∠BDA,进而得出∠MFO=∠ODA,tan∠MFO =tan∠ODA,故而![]() ,
,
即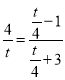 ,解出t的值,再求点E的坐标即可.
,解出t的值,再求点E的坐标即可.
(1)由题意可得:![]() ,
,
∴OA2=16,
∵OA>0,
∴OA=OB=4,
∴A(4,0),B(0,4).
(2)如图,过点E作EN⊥AC于点N.
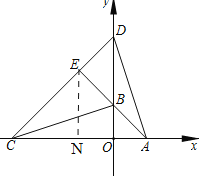
∵∠AOB=90°,OA=OB,
∴∠OAB=45°,
∵AB⊥CD,
∴∠CEA=90°,
∴∠ECA=45°,
∴△CEA是等腰直角三角形,
∵∠ECA=45°,∠COD=90°,
∴∠CDO=45°,
∴△CDO是等腰直角三角形.
∵点D纵坐标为t,
∴CO=DO=t.
∵OA=OB=4,
∴AC=t+4.
∴![]() ,
,
∴![]() ;
;
∴S与t的函数关系是:![]() .
.
(3)如图,过点F作FM⊥AC于点M,
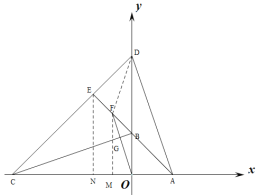
由(2)可知,![]() ,
,
∴![]() ,
,
∴点E的坐标为![]() ,
,
∵点B(0,4),点F为BE中点,
∴点F的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∵∠ABO=∠BDA+∠BAD=45°,∠FOB+∠DAE=45°,
∴∠FOB=∠BDA,
∴OF∥AD,
∵FM⊥AC,
∴FM∥DO,
∴∠MFO=∠ODA,
∴tan∠MFO =tan∠ODA,
∴![]() ,
,
即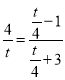 ,
,
解得t=12或4=-4(不合题意,舍去)
∴点E的坐标为![]() .
.

【题目】2019年4月23日世界读书日这天,滨江初二年级的学生会,就2018年寒假读课外书数量(单位:本)做了调查,他们随机调查了甲、乙两个班的10名同学,调查过程如下
收集数据
甲、乙两班被调查者读课外书数量(单位:本)统计如下:
甲:1,9,7,4,2,3,3,2,7,2
乙:2,6,6,3,1,6,5,2,5,4
整理、描述数据绘制统计表如下,请补全下表:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 4 | 3 | ||
乙 | 6 | 3.2 |
分析数据、推断结论
(1)该校初二乙班共有40名同学,你估计读6本书的同学大概有_____人;
(2)你认为哪个班同学寒假读书情况更好,写出理由.