题目内容
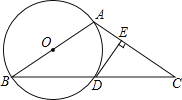
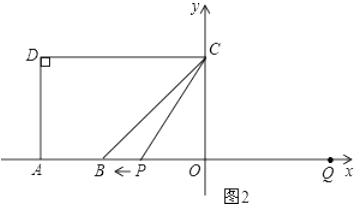
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.
(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
【答案】
(1)解:∵∠CBO=45°,
∴∠BCO=45°,
∴OC=OB,
又∵点C在y轴的正半轴上,
∴点C的坐标为(0,3),
(2)解:分两种情况讨论:
①点P在B点右侧时,如图2:
∵∠BCP=15°,∠BCO=45°,
∴∠OCP=45°-15°=30°,
在Rt△PCO中,设PO=x,则PC=2x,
∴PO2+OC2=PC2,
∴x2+32=(2x)2,
∴x=PO=![]() ,
,
又∵Q(4,0),
∴PQ=4+![]() ,
,
即t=4+![]() .
.
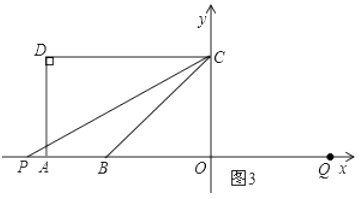
②点P在B点右侧时,如图3:
∵∠BCP=15°,∠BCO=45°,
∴∠OCP=45°+15°=60°,
∴∠CPO=30°,
在Rt△PCO中,
由(1)知OC=3,
∴PC=6,
∴PO2+OC2=PC2,
∴PO2+32=62,
∴PO=3![]() ,
,
又∵Q(4,0),
∴PQ=4+3![]() ,
,
即t=4+3![]() .
.
综上:t的值为:4+ ![]() 或4+3
或4+3 ![]()
(3)解: 依题可知:当⊙P与四边形ABCD的边(或边所在的直线)相切时,有以下三种情况:
①当⊙P与CB相切C点时(如图):
∴∠BCP=90°,
由(1)知∠BCO=45°,
∴∠OCP=45°,
∴Rt△PCO为等腰直角三角形,
∴CO=PO=3,
又∵Q(4,0),
∴PQ=1,
即t=1.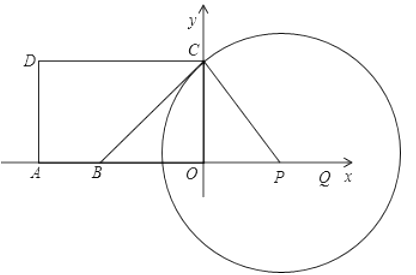
②当⊙P与CD相切于点C时(如图):
∴∠DCP=90°,
即点O与点P重合,
∴PQ=4,
即t=4.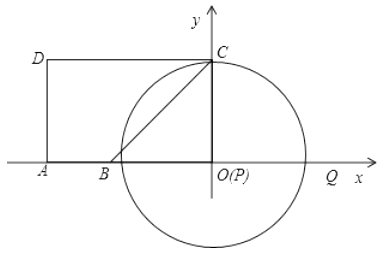
③当⊙P与AD相切于点A时(如图4):
∵Q(4,0),A(-5,0),
∴AQ=4-(-5)=9,
∴AP=PC=(9-t),PO=(t-4),
在Rt△PCO中,
∴PO2+CO2=PC2,
∴(t-4)2+32=(9-t)2,
∴t=5.6.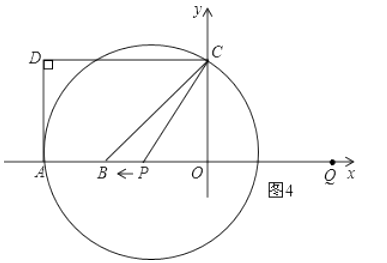
综上:t=1或4或5.6.
【解析】(1)由直角坐标系和三角形内角和定理得出∠CBO=∠BCO=45°,再根据等腰三角形性质得出OC=OB,从而得出C点坐标.
(2)分两种情况讨论:①点P在B点右侧时,如图2:由∠BCP=15°,∠BCO=45°得出∠OCP=30°,在Rt△PCO中,设PO=x,则PC=2x,
由勾股定理得出PO,从而求出t=4+![]() .
.
②点P在B点右侧时,如图3:由∠BCP=15°,∠BCO=45°得出∠OCP=60°,在Rt△PCO中,由直角三角形中,30度所对的直角边等于斜边的一半得出PC=6,由勾股定理得出PO,从而求出t=4+3![]() .
.
(3) 依题可知:当⊙P与四边形ABCD的边(或边所在的直线)相切时,有以下三种情况:
①当⊙P与CB相切C点时(如上图):根据切线性质得出∠BCP=90°,再由等腰直角三角形的性质得出CO=PO=3,从而求出t=1.
②当⊙P与CD相切于点C时(如上图):根据切线性质得出∠DCP=90°,即点O与点P重合,从而求出t=4.
③当⊙P与AD相切于点A时(如图4):由已知条件知AP=PC=(9-t),PO=(t-4),在Rt△PCO中由勾股定理求出t=5.6.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案