��Ŀ����
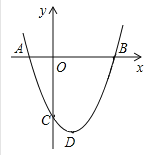
����Ŀ����ͼ���������� ABCD �У�E Ϊֱ�� AB �ϵĶ��㣨���� A��B �غ����������� DE ���Ƶ� D ��ʱ����ת 45������ֱ�� BC �ڵ� F������ EF��
̽�������� E �ڱ� AB �ϣ���֤��EF��AE+CF��
Ӧ�ã�(1)���� E �ڱ� AB �ϣ��� AD��2 ʱ������BEF ���ܳ���
(2)���� E �� BA �ӳ�����ʱ���ж� EF��AE��CF ���ߵ�������ϵ����˵�����ɣ�
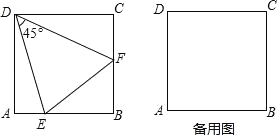
���𰸡�̽����֤����������Ӧ�ã�(1)��BEF ���ܳ�Ϊ4��(2)EF��CF��AE�����ɼ�����.
��������
̽�����������ߣ�����ȫ�������Σ�֤����DAG�ա�DCF��SAS��������1=��3��DG=DF����֤����GDE�ա�FDE��SAS��������EG�ij��ɵý��ۣ�
Ӧ�ã�
��1������̽���Ľ��ۼ����������ܳ�Ϊ4��
��2�����������������E��BA���ӳ�����ʱ��EF=CF-AE��������E��AB���ӳ�����ʱ�� EF=AE-CF��������������������ߣ�����ȫ�������Σ�֤����������ȫ�ȵ��߶���ȣ������߶εĺ����ó����ۣ�
̽����
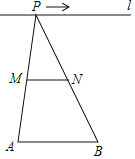
����ͼ���ӳ� BA �� G��ʹ AG��CF������ GD��

���ı��� ABCD Ϊ�����Σ���DA��DC����DAG����DCF��90�㣬
���DAG�ա�DCF��SAS����
���1����3��DG��DF��
�ߡ�DAC��90�㣬��EDF��45�㣬
���EDG����1+��2����3+��2��45�㣽��EDF��
��DE��DE��
���GDE�ա�FDE��SAS����
��EF��EG��AG+AE��AE+CF��
Ӧ�ã�
(1)��BEF ���ܳ���BE+BF+EF��
��̽���ã���BEF ���ܳ���BE+BF+EF��AB+BC��2+2��4��
(2)�� E �� BA ���ӳ�����ʱ������ͼ��

EF��CF��AE�������ǣ�
�� CB ��ȡ CG��AE������ DG��
�ߡ�DAE����DCG��90�㣬AD��DC��
���DAE�ա�DCG��SAS����
��DE��DG����EDA����GDC��
�ߡ�ADC��90�㣬��EDG��90�㣬
���EDF+��FDG��90�㣬
�ߡ�EDF��45�㣬
���FDG��90�㩁45�㣽45�㣬 ����EDF ����GDF �У�
DE��DG����EDF����GDF��DF��DF�����EDF�ա�GDF��SAS����
��FE��FG��
��EF��CF��CG��CF��AE��

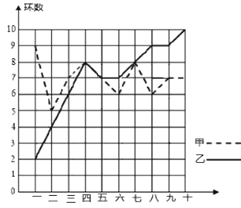
����Ŀ��ij�������������õ��շѷ�����
��ʱ��� | ��ͨ��� | |
��ʱ��8:00��21:00�� | ��ʱ��21:00������8:00�� | |
���0.55Ԫ/ǧ�ߡ�ʱ | ���0.35Ԫ/ǧ�ߡ�ʱ | ���0.52Ԫ/ǧ�ߡ�ʱ |
С�������ڵ�С���õĵ���������˷�ʱ���.
������⣺
��1��С����ͥij���õ�����Ϊ![]() ǧ�ߡ�ʱ��
ǧ�ߡ�ʱ��![]() Ϊ����������ʱ�õ�
Ϊ����������ʱ�õ�![]() ǧ�ߡ�ʱ����ʱ�õ�
ǧ�ߡ�ʱ����ʱ�õ�![]() ǧ�ߡ�ʱ����ʱ�Ƽ�ʱ�ܼ�Ϊ
ǧ�ߡ�ʱ����ʱ�Ƽ�ʱ�ܼ�Ϊ![]() Ԫ����ͨ�Ƽ�ʱ�ܼ�Ϊ
Ԫ����ͨ�Ƽ�ʱ�ܼ�Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() ���õ����ĺ�����ϵʽ.
���õ����ĺ�����ϵʽ.
��2��С����ͥʹ�÷�ʱ����Dz���һ������ͨ��������أ�
��3���±���·������������õ���վݣ�
��ʱ�õ磨ǧ�ߡ�ʱ�� | ��ʱ�õ磨ǧ�ߡ�ʱ�� |
181 | 239 |
�����ϱ��������÷�ʱ����Ƿ���㣿
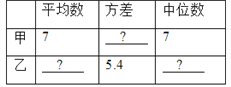
����Ŀ��ij����ʵʩ������ˮ�����ǰ���Ծ���������ˮ��������˵��飬�±���ͨ�������������õ�50����ͥȥ����ƽ����ˮ������λ���֣��������������ݽ�������������
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
Ƶ���ֲ���
���� | ���� | Ƶ�� |
2.0��x��3.5 | ���� | 11 |
3.5��x��5.0 |
| 19 |
5.0��x��6.5 | ||
6.5��x��8.0 | ||
8.0��x��9.5 |
| 2 |
�ϼ� | 50 |
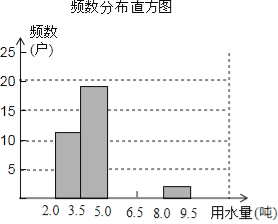
��1��������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
��2����ֱ��ͼ�����ܵõ�ʲô��Ϣ����д���������ɣ���
��3��Ϊ�˹�����Լ��ˮ��Ҫȷ��һ����ˮ���ı�������������IJ��ְ�1.5���۸��շѣ���Ҫʹ60%�ļ�ͥ�շѲ���Ӱ�죬����ü�ͥ�¾���ˮ��Ӧ�ö�Ϊ���٣�Ϊʲô��