题目内容
【题目】下面材料:
已知点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() 两点之间的距离表示为
两点之间的距离表示为![]()
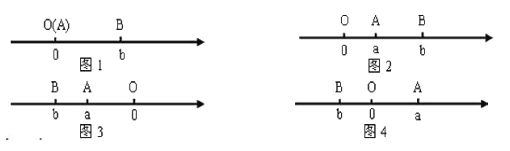
当![]() 两点中有一点在原点时,不妨设点
两点中有一点在原点时,不妨设点![]() 为原点,如图1,
为原点,如图1,![]()
当![]() 两点都不在原点时,
两点都不在原点时,
(1)如图2,点![]() 都在原点的右边,则
都在原点的右边,则![]()
(2)如图3,点![]() 都在原点的左边,则
都在原点的左边,则![]()
(3)如图4,点![]() 都在原点的两边,则
都在原点的两边,则![]()
综上,数轴上![]() 两点的距离
两点的距离![]()
回答下列问题:
(1)数轴上表示-2和5的两点之间的距离是 ;
(2)数轴上表示![]() 和-1的两点
和-1的两点![]() 之间的距离是
之间的距离是![]() ,如果
,如果![]() ,那么
,那么![]() ;
;
(3)拓展:若点![]() 表示的数为
表示的数为![]()
①则当![]() 为 时,
为 时,![]() 与
与![]() 的值相等.
的值相等.
②当![]() 时,整数
时,整数![]() 有 个
有 个
③![]() 的最小值是
的最小值是
④![]() 的最小值是
的最小值是
【答案】(1)![]() ;(2)0或-2;(3)①-1;②6;③2020;④20
;(2)0或-2;(3)①-1;②6;③2020;④20
【解析】
(1)根据两点间的距离公式计算即可解答.
(2)表示出A、B之间的距离,根据![]() 求出x的值即可.
求出x的值即可.
(3)①直接解答![]() =
=![]() ,求出a的值即可;
,求出a的值即可;
②由![]() 的意义是表示a到-2和3的点的距离之和是5,据此可得;
的意义是表示a到-2和3的点的距离之和是5,据此可得;
③由![]() 表示a到3和-2017的点距离之和,根据两点之间线段最短可得;
表示a到3和-2017的点距离之和,根据两点之间线段最短可得;
④![]() 表示a到1、2、3、4、5、6、7、8、9的点的距离之和,根据中点到线段两端的距离相等可得.
表示a到1、2、3、4、5、6、7、8、9的点的距离之和,根据中点到线段两端的距离相等可得.
(1)数轴上表示-2和5的两点之间的距离是![]()
(2)数轴上表示![]() 和-1的两点
和-1的两点![]() 之间的距离是
之间的距离是![]() ,如果
,如果![]() 可得:
可得:
![]() ,x=0或-2;
,x=0或-2;
(3)①![]() =
=![]() ;a=-1;
;a=-1;
②![]()
![]() 的意义是表示a到-2和3的点的距离之和是5,
的意义是表示a到-2和3的点的距离之和是5,
![]()
![]() ,其中整数有-2、-1、0、1、2、3共6个;
,其中整数有-2、-1、0、1、2、3共6个;
③![]() 表示a到3与-2017的点的距离之和,由两点之间线段最短可知:
表示a到3与-2017的点的距离之和,由两点之间线段最短可知:![]() 时,
时,![]() 有最小值,最小值为
有最小值,最小值为![]() .
.
④![]() 表示a到1、2、3、4、5、6、7、8、9的点的距离之和,根据中点到线段两端的距离相等可得:a=5时,
表示a到1、2、3、4、5、6、7、8、9的点的距离之和,根据中点到线段两端的距离相等可得:a=5时,![]() 有最小值,最小值为:
有最小值,最小值为:![]() .
.

练习册系列答案
相关题目