题目内容
【题目】如图,抛物线 y=ax2+bx﹣![]() 与 x 轴交于 A(1,0)、B(6,0)两点,D 是 y 轴上一点,连接 DA,延长 DA 交抛物线于点 E.
与 x 轴交于 A(1,0)、B(6,0)两点,D 是 y 轴上一点,连接 DA,延长 DA 交抛物线于点 E.
(1)求此抛物线的解析式;
(2)若 E 点在第一象限,过点 E 作 EF⊥x 轴于点 F,△ADO 与△AEF 的面积比为![]() =
=![]() ,求出点 E 的坐标;
,求出点 E 的坐标;
(3)若 D 是 y 轴上的动点,过 D 点作与 x 轴平行的直线交抛物线于 M、N 两点, 是否存在点 D,使 DA2=DMDN?若存在,请求出点 D 的坐标;若不存在,请说 明理由.

【答案】(1)抛物线的解析式为 y=﹣![]() x2+
x2+![]() x﹣
x﹣![]() ;(2)E 点坐标是(4,
;(2)E 点坐标是(4,![]() );(3)D 点坐标为(0,﹣
);(3)D 点坐标为(0,﹣![]() )或(0,3).
)或(0,3).
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据相似三角形的判定与性质,可得 AF 的长,根据自变量与函数值的对应关系,可得答案;
(3)根据两点间距离,可得 AD 的长,根据根与系数的关系,可得 x1x2,根据
DA2=DMDN,可得关于 n 的方程,解方程,即可得答案.
(1)将 A(1,0),B(6,0)代入函数解析式,得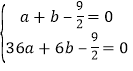 ,
,
解得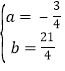 ,
,
抛物线的解析式为 y=﹣![]() x2+
x2+![]() x﹣
x﹣![]() ;
;
(2)∵EF⊥x 轴于点 F,
∴∠AFE=90°,
∵∠AOD=∠AFE=90°,∠OAD=∠FAE,
∴△AOD∽△AFE,
∵![]() =
=![]() =
=![]() ,
,
∵AO=1,
∴AF=3,OF=3+1=4,
当 x=4 时,y=﹣![]() ×42+
×42+![]() ×4﹣
×4﹣![]() =
=![]() ,
,
∴E 点坐标是(4,![]() );
);
(3)存在点 D,使 DA2=DMDN,理由如下:
设 D 点坐标为(0,n),
AD2=1+n2,
当 y=n 时,﹣![]() x2+
x2+![]() x﹣
x﹣![]() =n
=n
化简,得﹣3x2+21﹣18﹣4n=0, 设方程的两根为 x1,x2, x1x2=![]()
DM=x1,DN=x2,
DA2=DMDN,即 1+n2=![]() ,
,
化简,得
3n2﹣4n﹣15=0, 解得 n1=![]() ,n2=3,
,n2=3,
∴D 点坐标为(0,﹣![]() )或(0,3).
)或(0,3).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】数学老师在一次“探究性学习”课中,设计了如下数表:
| 2 | 3 | 4 | 5 | … |
| 3 | 8 | 15 | 24 | … |
| 4 | 6 | 8 | 10 | … |
| 5 | 10 | 17 | 26 | … |
由表可知,当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
………
(1)当![]() 时,
时,![]() ________,
________,![]() _________,
_________,![]() ________.
________.
(2)请你分别观察![]() ,
,![]() ,
,![]() 与
与![]() 之间的关系,并分别用含有
之间的关系,并分别用含有![]() 的代数式表示
的代数式表示 ![]() ,
,![]() ,
,![]() .
.
![]() ________,
________,![]() _________,
_________,![]() ________.
________.
(3)猜想以![]() ,
,![]() ,
,![]() 为边的三角形是否为直角三角形,并说明理由.
为边的三角形是否为直角三角形,并说明理由.