题目内容
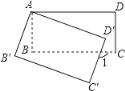
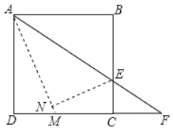
【题目】如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.
【答案】![]()
【解析】
先根据折叠的性质得∠EAB=∠EAN,AN=AB=8,再根据正方形的性质得AB∥CD,则∠EAB=∠F,所以∠EAN=∠F,得到MA=MF,设CM=x,则AM=MF=4+x,DM=DC-MC=8-x,在Rt△ADM中,根据勾股定理,解得x,然后利用MN=AM-AN求解即可.
解:∵△ABE沿直线AE翻折,点B落在点N处,
∴AN=AB=8,∠BAE=∠NAE,
∵正方形对边AB∥CD,
∴∠BAE=∠F,
∴∠NAE=∠F,
∴AM=FM,
设CM=x,∵AB=2CF=8,
∴CF=4,
∴DM=8﹣x,AM=FM=4+x,
在Rt△ADM中,由勾股定理得,AM2=AD2+DM2,
即(4+x)2=82+(8﹣x)2,
解得x=![]() ,
,
所以,AM=4+4![]() =8
=8![]() ,
,
所以,NM=AM﹣AN=8![]() ﹣8=
﹣8=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目