题目内容
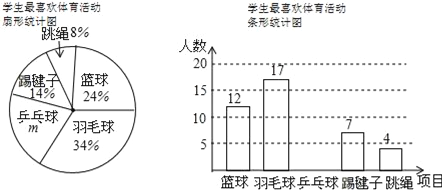
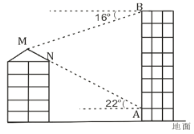
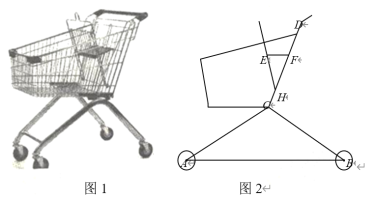
【题目】如图1是超市的手推车，如图2是其侧面示意图，已知前后车轮半径均为5 cm，两个车轮的圆心的连线AB与地面平行，测得支架AC＝BC＝60cm，AC、CD所在直线与地面的夹角分别为30°、60°，CD＝50cm．
（1）求扶手前端D到地面的距离；
（2）手推车内装有简易宝宝椅，EF为小坐板，打开后，椅子的支点H到点C的距离为10 cm，DF＝20cm，EF∥AB，∠EHD＝45°，求坐板EF的宽度．（本题答案均保留根号）
【答案】（1）35＋
；（2）坐板EF的宽度为（
）cm．
【解析】
（1）如图，构造直角三角形Rt△AMC、Rt△CGD然后利用解直角三角形分段求解扶手前端D到地面的距离即可；
（2）由已知求出△EFH中∠EFH＝60°，∠EHD＝45°，然后由HQ＋FQ＝FH＝20cm解三角形即可求解.
解：（1）如图2，过C作CM⊥AB，垂足为M，
又过D作DN⊥AB，垂足为N，过C作CG⊥DN，垂足为G，则∠DCG＝60°，
∵AC＝BC＝60cm，AC、CD所在直线与地面的夹角分别为30°、60°，∴∠A＝∠B＝30°，
则在Rt△AMC中，CM＝
＝30cm．
∵在Rt△CGD中，sin∠DCG＝
，CD＝50cm，
∴DG＝CDsin∠DCG＝50sin60°＝
＝，
又GN＝CM＝30cm，前后车轮半径均为5cm，
∴扶手前端D到地面的距离为DG＋GN＋5＝＋30＋5＝35＋（cm）．
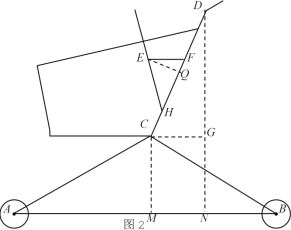
（2）∵EF∥CG∥AB，∴∠EFH＝∠DCG＝60°，
∵CD＝50cm，椅子的支点H到点C的距离为10cm，DF＝20cm，
∴FH＝20cm，
如图2，过E作EQ⊥FH，垂足为Q，设FQ＝x，
在Rt△EQF中，∠EFH＝60°，∴EF＝2FQ＝2x，EQ＝
，
在Rt△EQH中，∠EHD＝45°，∴HQ＝EQ＝
，
∵HQ＋FQ＝FH＝20cm，∴＋x＝20，解得x＝
，
∴EF＝2（）＝．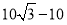
答：坐板EF的宽度为（）cm．
