��Ŀ����
����Ŀ�����Ķ����⣩
��A��B��CΪ���������㣬����C��A�ľ����ǵ�C��B�ľ����2�������ǾͳƵ�C�ǣ�A��B�����ŵ㣮
���磬��ͼ������A��ʾ����Ϊ��1����B��ʾ����Ϊ2����ʾ1�ĵ�C����A�ľ�����2������B�ľ�����1����ô��C�ǣ�A��B�����ŵ㣻���磬��ʾ0�ĵ�D����A�ľ�����1������B�ľ�����2����ô��D�Ͳ��ǣ�A��B�����ŵ㣬����D�ǣ�B��A�����ŵ㣮
��֪ʶ���ã�
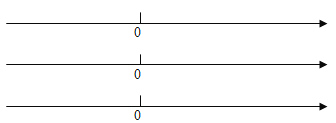
��ͼ�ڣ�M��NΪ���������㣬��M����ʾ����Ϊ��2����N����ʾ����Ϊ4��
��1������ ������ʾ�ĵ��ǣ�M��N�����ŵ㣻
��2����ͼ�ۣ�A��BΪ���������㣬��A����ʾ����Ϊ��20����B����ʾ����Ϊ40������һֻ��������P�ӵ�B��������4����λÿ����ٶ������˶��������Aֹͣ����tΪ��ֵʱ��P��A��B��ǡ��һ����Ϊ����������ŵ㣿

���𰸡���1��2��10����2����tΪ5�롢10���7.5��ʱ��P��A��B��ǡ��һ����Ϊ����������ŵ㣮
��������
��1����������Ϊx�������ŵ�Ķ�����ŵ���M��N֮����ŵ��ڵ�N�ұߣ��г����̽ⷽ�̼��ɣ���2�������ŵ�Ķ����֪�������������PΪ��A��B�����ŵ㣻��PΪ��B��A�����ŵ㣻��BΪ��A��P�����ŵ㣮���P��ʾ����Ϊx�������ŵ�Ķ����г����̣������ó�t��ֵ��
�⣺��1����������Ϊx��
���ŵ���M��N֮��ʱ���������x������2��=2��4��x�������x=2��
���ŵ��ڵ�N�ұ�ʱ���������x������2��=2��x��4������ã�x=10��
�ʴ�Ϊ��2��10��
��2�����P��ʾ����Ϊx����PA=x+20��PB=40��x��AB=40������20��=60��
�����������
��PΪ��A��B�����ŵ㣮
�����⣬��PA=2PB����x������20��=2��40��x����
���x=20��
��t=��40��20����4=5���룩��
��PΪ��B��A�����ŵ㣮
�����⣬��PB=2PA����40��x=2��x+20����
���x=0��
��t=��40��0����4=10���룩��
��BΪ��A��P�����ŵ㣮
�����⣬��AB=2PA����60=2��x+20��
���x=10��
��ʱ����PΪAB���е㣬��AҲΪ��B��P�����ŵ㣬
��t=30��4=7.5���룩��
���Ͽ�֪����tΪ5�롢10���7.5��ʱ��P��A��B��ǡ��һ����Ϊ����������ŵ㣮

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�