题目内容
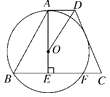
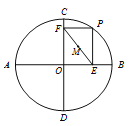
【题目】如图,AB、CD是⊙O的两条互相垂直的直径,P为⊙O上一动点,过点P分别作PE⊥AB、PF⊥CD,垂足分别为E、F,M为EF的中点.若点P从点B出发,以每秒15°的速度按逆时针方向旋转一周,当∠MAB 取得最大值时,点P运动的时间为______秒.
【答案】8或16
【解析】分析:根据题意,画出点P运动时的图形,找到变与不变的量,即可得出当当点P运动到AM与小圆O相切的位置时∠MAB 取得最大值,进而求出点P的旋转角度即可得出答案.
详解:如图所示,
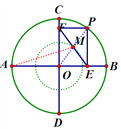
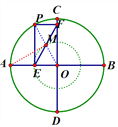

图1 图2 图3
由题可知四边形OEPF是矩形(点A、B、C、D处时为一条线段),
在点P运动的过程中,OP的长为圆O的半径长,
由矩形的性质可知,点M中OP的中点,
∴OM:AO=1:2,
当点P运动到AM与小圆O相切的位置时(图2、图3),∠MAB 取得最大值,
在Rt△AMO中,
∵OM:AO=1:2,
∴∠MAO=30°,
∴在图2中,可得∠POC=30°,在图3中可得∠POD=30°,
∴当点P从点B出发,以每秒15°的速度按逆时针方向旋转90°+30°=120°或270°-30°=240°时,∠MAB最大为30°,
∴点P运动的时间为:
![]() 或
或![]() .
.
故答案为:8或16.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目