题目内容
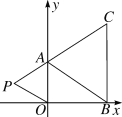
【题目】如图,点A(1,6)和点B在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5. 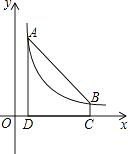
(1)求反比例函数的表达式和点B的坐标;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】
(1)解:∵点A(1,6)和点B在反比例函数图象上,
∴k=1×6=6,
∴反比例函数的表达式为:y= ![]() ;
;
∵AD⊥x轴于点D,
∴D(1,0),
∵BC⊥x轴于点C,DC=5.
∴B的横坐标为6,
将x=6代入y= ![]() 解得,y=1,
解得,y=1,
∴B(6,1)
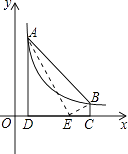
(2)解:存在,
设E(x,0),则DE=x﹣1,CE=6﹣x,
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
连接AE,BE,
则S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE
= ![]() (BC+AD)DC﹣
(BC+AD)DC﹣ ![]() DEAD﹣
DEAD﹣ ![]() CEBC
CEBC
= ![]() ×(1+6)×5﹣
×(1+6)×5﹣ ![]() (x﹣1)×6﹣
(x﹣1)×6﹣ ![]() (6﹣x)×1
(6﹣x)×1
= ![]() ﹣
﹣ ![]() x=5,
x=5,
解得:x=5,
则E(5,0).
【解析】(1)根据待定系数法即可求得反比例函数的解析式组,进而确定出B横坐标坐标,横坐标代入即可确定出纵坐标;(2)存在,设E(x,0),表示出DE与CE,连接AE,BE,三角形ABE面积=四边形ABCD面积﹣三角形ADE面积﹣三角形BCE面积,求出即可.
【考点精析】通过灵活运用比例系数k的几何意义,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积即可以解答此题.

练习册系列答案
相关题目