题目内容
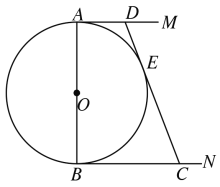
【题目】如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD= ![]() ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 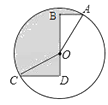
【答案】![]()
【解析】在Rt△ABO中,∠ABO=90°,OA=2,AB=1,
∴OB= ![]() =
= ![]() ,sin∠AOB=
,sin∠AOB= ![]() ,∠AOB=30°.
,∠AOB=30°.
同理,可得出:OD=1,∠COD=60°.
∴∠AOC=∠AOB+(180°-∠COD)=30°+180°-60°=150°.
在△AOB和△OCD中,有 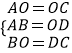 ,
,
∴△AOB≌△OCD(SSS).
∴S阴影=S扇形OAC .
∴S扇形OAC= ![]() πR2=
πR2= ![]() π×22=
π×22= ![]() π.
π.
在直角三角形中,由AB=1,CD= ![]() ,半径为2,利用三角函数,可求出sin∠AOB,sin∠COD,进而得出△AOB≌△OCD,把阴影部分面积转化为规则的扇形面积,利用扇形面积公式可求出面积.
,半径为2,利用三角函数,可求出sin∠AOB,sin∠COD,进而得出△AOB≌△OCD,把阴影部分面积转化为规则的扇形面积,利用扇形面积公式可求出面积.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目