题目内容
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
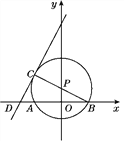
【答案】(1)C(-2,2);(2)证明见解析.
【解析】试题分析:
(1)Rt△OBP中,由勾股定理得到OP的长,连接AC,因为BC是直径,所以∠BAC=90°,因为OP是△ABC的中位线,所以OA=2,AC=2,即可求解;
(2)由点C的坐标可得直线CD的解析式,则可求点D的坐标,从而可用SAS证△DAC≌△POB,进而证∠ACB=90°.
试题解析:
(1)解:如图,连接CA.∵OP⊥AB,∴OB=OA=2.∵OP2+BO2=BP2,
∴OP2=5-4=1,OP=1.∵BC是⊙P的直径,∴∠CAB=90°.
∵CP=BP,OB=OA,∴AC=2OP=2.∴B(2,0),P(0,1),C(-2,2).
(2)证明:∵直线y=2x+b过C点,∴b=6.∴y=2x+6.
∵当y=0时,x=-3,∴D(-3,0).∴AD=1.∵OB=AC=2,AD=OP=1,
∠CAD=∠POB=90°,∴△DAC≌△POB.∴∠DCA=∠ABC.
∵∠ACB+∠CBA=90°,∴∠DCA+∠ACB=90°,即CD⊥BC.∴CD是⊙P的切线.

练习册系列答案
相关题目