题目内容
【题目】如图，ABCD绕点A逆时针旋转30°，得到□AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=（ ）
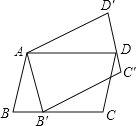
A. 105°B. 170°C. 155°D. 145°
【答案】A
【解析】
先根据旋转的性质得到AB=AB′，∠BAB′=30°，再根据等腰三角形的性质和三角形内角和定理可得到∠B=∠AB′B=75°，然后根据平行四边形的性质得
AB∥CD，再根据平行线的性质计算得∠C=180°-∠B=105°．
∵ABCD绕点A逆时针旋转30°，得到□AB′C′D′′，
∴AB=AB′，∠BAB′=30°，
∴∠B=∠AB′B=
（180°-30°）=75°，
∵四边形ABCD为平行四边形，
∴AB∥CD，
∴∠B+∠C=180°，
∴∠C=180°-75°=105°．
故选A．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某商场计划用3300元购进甲，乙两种商品共100个，这两种商品的进价、售价如下表：
进价（元/个） | 售价（元/个） | |
甲种 | 25 | 30 |
乙种 | 45 | 60 |
（1）求甲、乙两种商品各进多少个？
（2）全部售完100个商品后，该商场获利多少元？
