题目内容
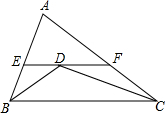
已知：如图，OA平分∠BAC，∠1=∠2．
求证：△ABC是等腰三角形．
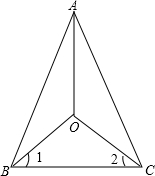
求证：△ABC是等腰三角形．
证明：作OE⊥AB于E，OF⊥AC于F，
∵AO平分∠BAC，
∴OE=OF（角平分线上的点到角两边的距离相等）．
∵∠1=∠2，
∴OB=OC．
∴Rt△OBE≌Rt△OCF（HL）．
∴∠5=∠6．
∴∠1+∠5=∠2+∠6．
即∠ABC=∠ACB．
∴AB=AC．
∴△ABC是等腰三角形．
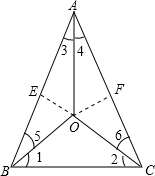
∵AO平分∠BAC，
∴OE=OF（角平分线上的点到角两边的距离相等）．
∵∠1=∠2，
∴OB=OC．
∴Rt△OBE≌Rt△OCF（HL）．
∴∠5=∠6．
∴∠1+∠5=∠2+∠6．
即∠ABC=∠ACB．
∴AB=AC．
∴△ABC是等腰三角形．
练习册系列答案
天天练口算系列答案
相关题目
