题目内容
在平面直角坐标系xOy中,关于y轴对称的抛物线y=-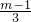 x2+(m-2)x+4m-7与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,P是这条抛物线上的一点(点P不在坐标轴上),且点P关于直线BC的对称点在x轴上,D(0,3)是y轴上的一点.
x2+(m-2)x+4m-7与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,P是这条抛物线上的一点(点P不在坐标轴上),且点P关于直线BC的对称点在x轴上,D(0,3)是y轴上的一点.
(1)求抛物线的解析式及点P的坐标;
(2)若E、F是 y 轴负半轴上的两个动点(点E在点F的上面),且EF=2,当四边形PBEF的周长最小时,求点E、F的坐标;
(3)若Q是线段AC上一点,且S△COQ=2S△AOQ,M是直线DQ上的一个动点,在x轴上方的平面内存在一点N,使得以 O、D、M、N为顶点的四边形是菱形,请你直接写出点N的坐标
解:(1)∵抛物线 +(m-2)x+4m-7关于y轴对称,
+(m-2)x+4m-7关于y轴对称,
∴m-2=0.
∴m=2.
∴抛物线的解析式是y=-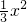 +1
+1
令y=0,得x=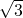
∴A(- ,0),B(
,0),B( ,0)
,0)
在Rt△BOC中,OC=1,OB= ,可得∠OBC=30°.
,可得∠OBC=30°.
在Rt△BOD中,OD=3,OB= ,可得∠OBD=60°.
,可得∠OBD=60°.
∴BC是∠OBD的角平分线.
∴直线BD与x轴关于直线BC对称.
因为点P关于直线BC的对称点在x轴上,
则符合条件的点P就是直线BD与抛物线y=-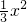 +1的交点.
+1的交点.
设直线BD的解析式为y=kx+b.
∴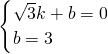 ,
,
∴ ,
,
∴直线BD的解析式为
∵点P在直线BD上,设P点坐标为
又因为点P在抛物线y=-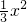 +1上,
+1上,
∴ =-
=-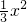 +1
+1
∴ .
.
∴y1=0,y2=-3
∴点P的坐标是 .
.
(2)过点P作PG⊥x轴于G,在PG上截取PH=2,连接AH与y轴交于点E,在y轴的负半轴上截取EF=2.

∵PH∥EF,PH=EF,
∴四边形PHEF为平行四边形,有HE=PF.
又∵PB、EF的长为定值,
∴此时得到的点E、F使四边形PBEF的周长最小.
∵OE∥GH,
∴Rt△AOE∽Rt△AGH.
∴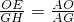 .
.
∴OE= =
= .
.
∴OF=OE+EF= +2=
+2= .
.
∴点E的坐标为(0,- ),点F的坐标为(0,-
),点F的坐标为(0,- ).
).
(3)点N的坐标是 )或
)或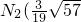
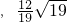 )或
)或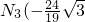 ,
, .
.
分析:(1)本题需先根据已知条件求出抛物线的解析式,再根据A、B两点求出∠OBC的度数和∠OBD的度数,再证出直线BD与x轴关于直线BC对称,再设直线BD的解析式为y=kx+b,再把各点代入,最后求出结果即可.
(2)本题可先过点P作PG⊥x轴于G,在PG上截取PH=2,证出四边形PHEF为平行四边形得出HE=PF,再根据已有的条件证出Rt△AOE∽Rt△AGH,最后即可求出点E、F的坐标.
(3)本题根据已有的条件,再结合图形,可以直接写出点N的坐标.
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合的数学思想方法.
 +(m-2)x+4m-7关于y轴对称,
+(m-2)x+4m-7关于y轴对称,∴m-2=0.
∴m=2.
∴抛物线的解析式是y=-
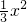 +1
+1令y=0,得x=
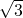
∴A(-
 ,0),B(
,0),B( ,0)
,0)在Rt△BOC中,OC=1,OB=
 ,可得∠OBC=30°.
,可得∠OBC=30°.在Rt△BOD中,OD=3,OB=
 ,可得∠OBD=60°.
,可得∠OBD=60°.∴BC是∠OBD的角平分线.
∴直线BD与x轴关于直线BC对称.
因为点P关于直线BC的对称点在x轴上,
则符合条件的点P就是直线BD与抛物线y=-
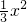 +1的交点.
+1的交点.设直线BD的解析式为y=kx+b.
∴
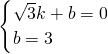 ,
,∴
 ,
,∴直线BD的解析式为

∵点P在直线BD上,设P点坐标为

又因为点P在抛物线y=-
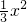 +1上,
+1上,∴
 =-
=-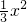 +1
+1∴
 .
.∴y1=0,y2=-3
∴点P的坐标是
 .
.(2)过点P作PG⊥x轴于G,在PG上截取PH=2,连接AH与y轴交于点E,在y轴的负半轴上截取EF=2.

∵PH∥EF,PH=EF,
∴四边形PHEF为平行四边形,有HE=PF.
又∵PB、EF的长为定值,
∴此时得到的点E、F使四边形PBEF的周长最小.
∵OE∥GH,
∴Rt△AOE∽Rt△AGH.
∴
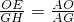 .
.∴OE=
 =
= .
.∴OF=OE+EF=
 +2=
+2= .
.∴点E的坐标为(0,-
 ),点F的坐标为(0,-
),点F的坐标为(0,- ).
).(3)点N的坐标是
 )或
)或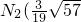
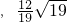 )或
)或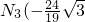 ,
, .
.分析:(1)本题需先根据已知条件求出抛物线的解析式,再根据A、B两点求出∠OBC的度数和∠OBD的度数,再证出直线BD与x轴关于直线BC对称,再设直线BD的解析式为y=kx+b,再把各点代入,最后求出结果即可.
(2)本题可先过点P作PG⊥x轴于G,在PG上截取PH=2,证出四边形PHEF为平行四边形得出HE=PF,再根据已有的条件证出Rt△AOE∽Rt△AGH,最后即可求出点E、F的坐标.
(3)本题根据已有的条件,再结合图形,可以直接写出点N的坐标.
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合的数学思想方法.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
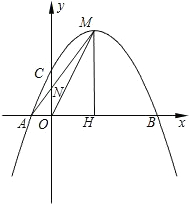 直线QG的解析式;若不存在,请说明理由.
直线QG的解析式;若不存在,请说明理由.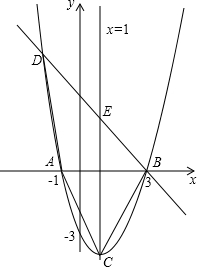 点B在A点的右侧;交y轴于(0,-3).
点B在A点的右侧;交y轴于(0,-3).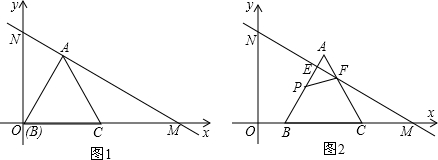
 ,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为
,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为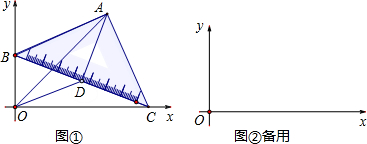 如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.