��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y= ![]() ��x��m��2��
��x��m��2�� ![]() m2+m�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
m2+m�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ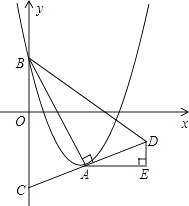
��1����m=2ʱ�����B�����ꣻ
��2����DE�ij���
��3�������D������Ϊ��x��y������y����x�ĺ�����ϵʽ���ڹ���D��AB��ƽ���ߣ���ڣ�3������ȷ���ĺ���ͼ�����һ������ΪP����mΪ��ֵʱ����A��B��D��PΪ������ı�����ƽ���ı��Σ�
���𰸡�
��1��
�⣺��m=2ʱ��y= ![]() ��x��2��2+1��
��x��2��2+1��
��x=0����y= ![]() ��x��2��2+1���ã�y=2��
��x��2��2+1���ã�y=2��
���B��������0��2��
��2��
�⣺�ӳ�EA����y���ڵ�F��
��AD=AC����AFC=��AED=90�㣬��CAF=��DAE��
���AFC�ա�AED��
��AF=AE��
�ߵ�A��m���� ![]() m2+m������B��0��m����
m2+m������B��0��m����
��AF=AE=|m|��BF=m������ ![]() m2+m��=
m2+m��= ![]() m2��
m2��
�ߡ�ABF=90�㩁��BAF=��DAE����AFB=��DEA=90�㣬
���ABF�ס�DAE��
�� ![]() ������
������ ![]() =
= ![]() ��
��
��DE=4��
��3��
�⣺�١ߵ�A������Ϊ��m���� ![]() m2+m����
m2+m����
���D��������2m���� ![]() m2+m+4����
m2+m+4����
��x=2m��y=�� ![]() m2+m+4��
m2+m+4��
��y=�� ![]()
![]() +
+ ![]() +4��
+4��
���������Ľ���ʽΪ��y=�� ![]() x2+
x2+ ![]() x+4��
x+4��
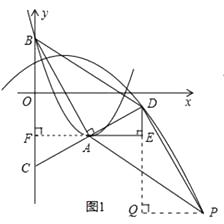
����PQ��DE�ڵ�Q�����DPQ�ա�BAF��
��i�����ı���ABDPΪƽ���ı���ʱ����ͼ1����
��P�ĺ�����Ϊ3m��
��P�������������� ![]() m2+m+4������
m2+m+4������ ![]() m2��=��
m2��=�� ![]() m2+m+4��
m2+m+4��
��P��3m���� ![]() m2+m+4�����������y=��
m2+m+4�����������y=�� ![]() x2+
x2+ ![]() x+4�ã�
x+4�ã�
�� ![]() m2+m+4=��
m2+m+4=�� ![]() ����3m��2+
����3m��2+ ![]() ����3m��+4��
����3m��+4��
��ã�m=0����ʱA��B��D��P��ͬһֱ���ϣ���ȥ����m=8��
��ii�����ı���ABPDΪƽ���ı���ʱ����ͼ2����
��P�ĺ�����Ϊm��
��P�������������� ![]() m2+m+4��+��
m2+m+4��+�� ![]() m2��=m+4��
m2��=m+4��
��P��m��m+4�����������y=�� ![]() x2+
x2+ ![]() x+4�ã�
x+4�ã�
m+4=�� ![]() m2+
m2+ ![]() m+4��
m+4��
��ã�m=0����ʱA��B��D��P��ͬһֱ���ϣ���ȥ����m=��8��
����������m��ֵΪ8��8��
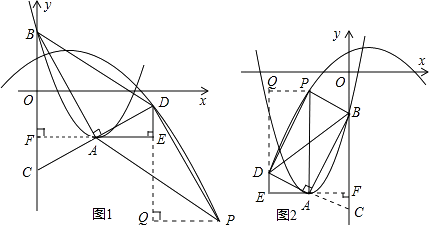
����������1����m=2����ԭʽ���õ����κ����Ķ���ʽ���ݴ˼������B������ꣻ��2���ӳ�EA����y���ڵ�F��֤����AFC�ա�AED������֤����ABF�ס�DAE���������������ε����ʣ����DE=4����3���ٸ��ݵ�A�͵�B�����꣬�õ�x=2m��y=�� ![]() m2+m+4����m=
m2+m+4����m= ![]() ����y=��
����y=�� ![]() m2+m+4������������κ����ı���ʽ��
m2+m+4������������κ����ı���ʽ��
����PQ��DE�ڵ�Q�����DPQ�ա�BAF��Ȼ��֣���ͼ1���ͣ�ͼ2������������
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�