Question

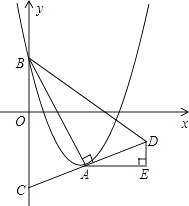
【题目】如图，Rt△ABC中，∠B=90°，AB=6，BC=9，将△ABC折叠，使点C与AB的中点D重合，折痕交AC于点M，交BC于点N．

（1）求线段BN的长；

（2）连接CD，与MN交于点E，写出与点E相关的两个正确结论：①　 　；

②　 　．

Answer 1

【答案】（1）4;（2）DE=EC，∠DEM=90°.

【解析】

先求得BD的长，设BF=x，由翻折的性质可知：DF=9-x．接下来，在Rt△BDF中，由勾股定理可列出关于x的方程求解即可．

解：（1）∵D是AB的中点，

∴BD=AB=3．

设BF=x，则CF=9﹣x．

由翻折的性质可知：DF=CF=9﹣x．

在△BDF中，由勾股定理得：DF2=BD2+FB2，即（9﹣x）2=32+x2．

解得：x=4．

∴BF的长为4．

（2）如图：结论：①DE=EC；②∠DEM=90°，

故答案为DE=EC，∠DEM=90°