题目内容
【题目】 在等腰Rt△ABC中,∠C=90°,AC=BC,点M,N分别是边AB,BC上的动点,△BMN与△B′MN关于直线MN对称,点B的对称点为B′.
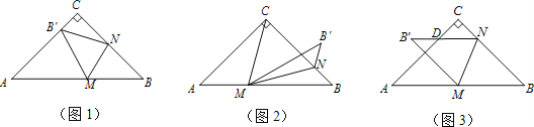
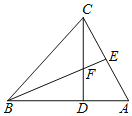
(1)如图1,当B′在边AC上时,若∠CNB′=25°,求∠AMB′的度数;
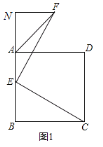
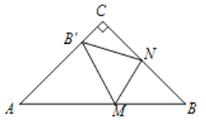
(2)如图2,当∠BMB′=30°且CN=MN时,若CMBC=2,求△AMC的面积;
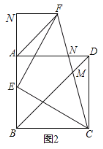
(3)如图3,当M是AB边上的中点,B′N交AC于点D,若B′N∥AB,求证:B′D=CN.
【答案】(1)65°;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由△MNB′是由△MNB翻折得到,推出∠B=∠MB′N=45°,∠MNB=∠MNB′=![]() (180°-25°)=77.5°,推出∠NMB=∠NMB′=57.5°,可得∠BMB°=115°解决问题.
(180°-25°)=77.5°,推出∠NMB=∠NMB′=57.5°,可得∠BMB°=115°解决问题.
(2)如图2,作MH⊥AC于H.首先证明![]() ,推出S△ACM=
,推出S△ACM=![]() 即可解决问题.
即可解决问题.
(3)如图3,设AM=BM=a,则AC=BC=![]() a.通过计算证明CN=DB′即可.
a.通过计算证明CN=DB′即可.
(1)如图,
∵∠C=90°,CA=CB,
∴∠A=∠B=45°,
∵△MNB′是由△MNB翻折得到,
∴∠B=∠MB′N =45°,∠MNB=∠MNB′=![]() (180°-25°)=77.5°,
(180°-25°)=77.5°,
∴∠NMB=∠NMB′=57.5°,
∴∠BM B′=115°,
∴∠AMB′=180°-115°=65°;
(2)∵△MNB′是由△MNB翻折得到,∠BMB′=30°,
∴∠BMN=∠NMB′=15°,
∵∠B=45°,
∴∠CNM=∠B+∠NMB=60°,
∵CN=MN,
∴△CMN是等边三角形,
∴∠MCN=60°,
∵∠ACB=90°,
∴∠ACM=30°,
如图,作MH⊥AC于H.
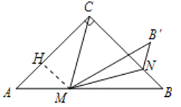
∴∠MHC=90°,
∴MH=![]() CM,
CM,
∵S△ACM=![]() AC
AC![]() MH=
MH=![]() BC
BC![]() CM=
CM=![]() CM
CM![]() BC=
BC=![]() ;
;
(3)如图,设AM=BM=a,则AC=BC=![]() a.
a.
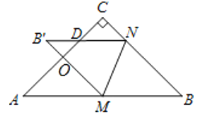
∵NB′∥AB,
∴∠CND=∠B=45°,∠MND=∠NMB,
∵∠MNB=∠MND,
∴∠NMB =∠MNB,
∴MB=BN=a,
∴CN=![]() a-a,
a-a,
∵∠C=90°,
∴∠CDN=∠CND=45°,
∴CD=CN,
∵CA=CB,
∴AD=BN=a,
设AD交MB′于点O,
∵MB=BN,∠B=45°,
∴∠BMN=![]() ,
,
∵△MNB′是由△MNB翻折得到,
∴∠BMN=∠NMB′=![]() ,
,
∴∠AMO=180![]() ∠BMN
∠BMN![]() ∠NMB′=180
∠NMB′=180![]() ,
,
∴![]() 是等腰直角三角形,且AM=a,
是等腰直角三角形,且AM=a,
∴AO=OM=![]() a,OB′=OD=a-
a,OB′=OD=a-![]() a,
a,
∴DB′=![]() OD=
OD=![]() a-a,
a-a,
∴B′D=CN.

 天天向上口算本系列答案
天天向上口算本系列答案【题目】 某公司的一批某品牌衬衣的质量抽检结果如下:
抽检件数 | 50 | 100 | 200 | 300 | 400 | 500 |
次品件数 | 0 | 4 | 16 | 19 | 24 | 30 |
(1)请结合表格数据直接写出这批衬衣中任抽1件是次品的概率.
(2)如果销售这批衬衣600件,至少要准备多少件正品衬衣供买到次品的顾客退换?