题目内容
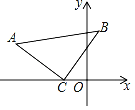
【题目】如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,连接EC,则∠BCE=°. 
【答案】65
【解析】解:∵四边形ABCD是正方形,
∴AB=CB(正方形的四条边相等),∠ABE=CBE(正方形的对角线平分每一组对角),
∴在△ABE和△CBE中,
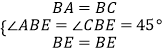 ,
,
∴△ABE≌△CBE,
∴∠BCE=∠BAE,
∵∠DAF=25°,
∴∠BAE=90°﹣25°=65°,
∴∠BCE=65°.
所以答案是:65°.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目
【题目】八(1)班组织了一次食品安全知识竞赛,甲、乙两队各5人的成绩如表所示(10分制).
甲 | 8 | 10 | 9 | 6 | 9 |
乙 | 10 | 8 | 9 | 7 | 8 |
(1)甲队成绩的中位数是分;
(2)乙队成绩的众数是分;
(3)分别计算甲队、乙队的方差;并判断哪队的成绩更稳定?为什么?