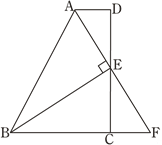
题目内容
【题目】如图,AD, CE为ΔABC的角平分线且交于0点,∠DAC=30°,∠ECA=35°,则∠AOB=_______。

【答案】125°
【解析】
根据角平分线的定义可得出∠BAC=60°、∠ACB=70°,结合三角形内角和可得出∠ABC=50°,由三角形的三条角平分线交于一点,可得出BO平分∠ABC,进而可得出∠ABO的度数,进而可求出∠AOB的度数.
解:∵AD平分∠BAC,CE平分∠ACB,∠DAC=30°,∠ECA=35°,
∴BAD=∠DAC=30°,,∠BAC=2∠DAC=60°,∠ACB=2∠ECA=70°,
∴∠ABC=180°-∠BAC-∠ACB=50°.
∵△ABC的三条角平分线交于一点,
∴BO平分∠ABC,
∴∠ABO=![]() ∠ABC=25°,
∠ABC=25°,
∴∠AOB=180°-30°-25°=125°.
故答案为:125°.

 名校课堂系列答案
名校课堂系列答案【题目】某校初二年级数学考试,(满分为100分,该班学生成绩均不低于50分)作了统计分析,绘制成如图频数分布直方图和频数、频率分布表,请你根据图表提供的信息,解答下列问题:
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | a | 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |

(1)频数、频率分布表中a= ,b= ;(答案直接填在题中横线上)
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
【题目】小华有一个容量为8GB (1GB= 1024MB)的U盘,U盘中已经存储了一个视频文件,其余空间都用来存储照片,若每张照片占用的内存容量均相同,图片数量x (张)和剩余可用空间y (MB)的部分关系如表:
图片数量 | 100 | 150 | 200 | 400 | 800 |
剩余可用空间 | 5700 | 5550 | 5400 | 4800 | 3600 |
(1)由上表可知,y与x之间满足___ ___(填“一次”或“二次”或“反比例”)函数的关系,求出y与x之间的关系式.
(2)求出U盘中视频文件的占用内存容量.