题目内容
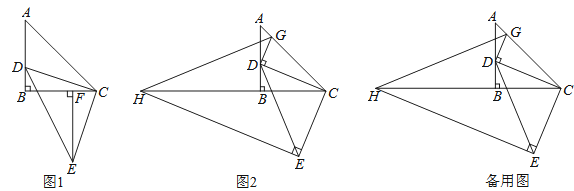
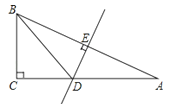
【题目】如图,△AOB中,A(-8,0),B(0, ![]() ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,
(1)⊙P的半径为 ;
(2)求证:EF为⊙P的切线;
(3)若点H是![]() 上一动点,连接OH、FH,当点H在
上一动点,连接OH、FH,当点H在![]() 上运动时,试探究
上运动时,试探究![]() 是否为定值?若为定值,求其值;若不是定值,请说明理由.
是否为定值?若为定值,求其值;若不是定值,请说明理由.

【答案】(1)5;(2)证明见解析;(3)![]() 是定值,
是定值, ![]()
【解析】试题分析:(1)根据勾股定理求得AB=![]() ,根据角平分线上的点到角两边的距离相等,得到AE=AO=8,BE=
,根据角平分线上的点到角两边的距离相等,得到AE=AO=8,BE=![]() ,在△BEC中,根据勾股定理求得CO=CE=4,再依据△AOC∽△COD求得OD=2,进而求得半径为5;(2)依据角平分线证得PC//AE,得到CP⊥EF;(3)根据△POH∽△PHF求得
,在△BEC中,根据勾股定理求得CO=CE=4,再依据△AOC∽△COD求得OD=2,进而求得半径为5;(2)依据角平分线证得PC//AE,得到CP⊥EF;(3)根据△POH∽△PHF求得![]() .
.
试题解析:
(1)5
(2)证明:连接CP,
∵AP=CP
∴∠PAC=∠PCA
∵AC平分∠OAB
∴∠PAC=∠EAC
∴∠PCA=∠EAC
∴PC//AE
∵CE⊥AB
∴CP⊥EF即EF是⊙P的切线
(3)![]() 是定值,
是定值, ![]()
连接PH,
由(1)得AP=PC=PH=5,∵A(-8,0) ∴OA=8 ∴OP=OA-AP=3
在Rt△POC中, ![]()
由射影定理可得![]() ,∴OF=
,∴OF=![]() , ∴PF=PO+OF=
, ∴PF=PO+OF=![]()
∵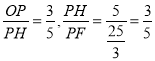 , ∴
, ∴![]() 又∵∠HPO=∠FPH
又∵∠HPO=∠FPH
∴△POH∽△PHF
∴![]() ,
,
当H与D重合时, ![]() .
.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目