题目内容
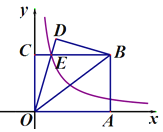
【题目】如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线![]() 经过点E,则k=_____;
经过点E,则k=_____;
【答案】![]()
【解析】由翻折可知BD=OC, ∠D=∠BCO, 又∵∠CEO=∠DEB,
∴△COE∽△DBE.
∴OE=BE,
设CE=x,则OE=8-x,
在Rt△COE中,根据勾股定理得OC+CE=OE,即3+x=(4-x),解得![]() ,
,
∴k=![]() .
.
点睛:折叠与翻折类试题主要有四个特点:(1)折叠与翻折类试题常常与线段垂直平分线,等腰三角形,全等三角形,相似三角形,解直角三角形等内容结合在一起;(2)在折叠与翻折的过程中寻找不变量,在折叠与翻折的过程中挖掘新生成的特殊图形(或常见的基本图形),立足翻折不变量,考查翻折的新生成;(3)将方程,锐角三角函数,解直角三角形和折叠与翻折融合在一起考查;(4)直角,中点,角平分线,相似三角形,锐角三角函数,解直角三角形,方程思想,转化与化归是解决折叠与翻折问题的常见关键词.

练习册系列答案
相关题目

