ћвƒњƒЏ»Ё
°Њћвƒњ°њќ™ЅЋљвќ“ѕЎ÷–—І…ъ≤ќЉ”°∞–¬єЏЈќ—„÷™ ґ°±ЊЇ»ь≥…Љ®µƒ«йњц£ђЋжїъ≥й≤йЅЋ≤њЈ÷≤ќ»ь—І…ъµƒ≥…Љ®£ђЄщЊЁ≥…Љ®Ј÷≥…»зѕ¬ЋƒЄц„й£ЇA£Ї60°№x£Љ70£ђB£Ї70°№x£Љ80£ђC£Ї80°№x£Љ90£ђD£Ї90°№x°№100£ђ≤Ґ÷∆„ч≥ц»зѕ¬µƒ…»–ќЌ≥Љ∆ЌЉЇЌ÷±ЈљЌЉ£Ѓ«лЄщЊЁЌЉ±н–≈ѕҐљвірѕ¬Ѕ–ќ ћв£Ї
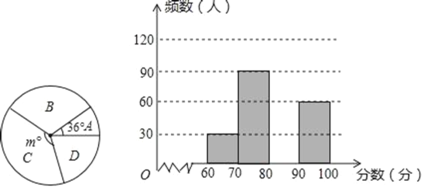
£®1£©…»–ќЌ≥Љ∆ЌЉ÷–µƒm£љ°° °°£ђ≤Ґ‘ЏЌЉ÷–≤є»Ђ∆µ эЈ÷≤Љ÷±ЈљЌЉ£ї
£®2£©–°√чµƒ≥…Љ® «Ћщ”–±ї≥й≤й—І…ъ≥…Љ®µƒ÷–ќї э £ђЊЁіЋЌ∆ґѕЋыµƒ≥…Љ®‘Џ°° „й£ї
£®3£©4Єц–°„й√њ„йЌ∆Љц1»Ћ£ђ»їЇуі”4»Ћ÷–Ћжїъ≥й»°2»Ћ≤ќЉ”∞дљ±µдјс£ђ«°Ї√≥й÷–A£ђCЅљ„й—І…ъµƒЄ≈¬ «ґа…ў£њ«лЅ–±нїтї≠ ч„іЌЉЋµ√ч£ї
£®4£©»фќ“ѕЎ—І…ъ»Ћ эќ™18000»Ћ£ђ«лЄщЊЁ…ѕ цµч≤йљбєы£ђєјЉ∆ќ“ѕЎ—І…ъ≥…Љ®‘ЏC°ҐDЅљ„йµƒє≤ґа…ў»Ћ£Ѓ
°Њір∞Є°њ£®1£©300£ђ≤єЌЉЉыљвќц£ї£®2£©144£ђC£ї£®3£©![]() £ї£®4£©1080£Ѓ
£ї£®4£©1080£Ѓ
°Њљвќц°њ
£®1£©ѕ»јы”√A„йµƒ∆µ э”лЋьЋщ’Љµƒ∞ўЈ÷±»Љ∆Ћг≥цµч≤йµƒ„№»Ћ э£ђ‘ўЉ∆Ћг≥цC„й»Ћ э£ђ»їЇу”√360≥Ћ“‘C„йЋщ’Љµƒ∞ўЈ÷±»µ√µљmµƒ÷µ£ђ„оЇу≤є»Ђ∆µ эЌ≥Љ∆ЌЉ£ї
£®2£©јы”√÷–ќї эµƒґ®“ељш––≈–ґѕ£ї
£®3£©Ќ®єэЅ–±н’є ЊЋщ”–12÷÷µ»њ…ƒ№љбєы£ђ‘ў’“≥ц≥йµљA°ҐC„й»Ћµƒљбєы э£ђ»їЇуЄщЊЁЄ≈¬ єЂ љ«уљв£Ѓ
£®4£©”√C,DЅљ„йµƒЋщ’Љ∞ўЈ÷±»µƒЇЌ≥Ћ“‘18000Љіњ…«у.
£®1£©µч≤йµƒ„№»Ћ эќ™30°¬![]() £љ300£®»Ћ£©£ђ
£љ300£®»Ћ£©£ђ
C„й»Ћ эќ™300©Б30©Б90©Б60£љ120£®»Ћ£©£ђ
Ћщ“‘m£љ360°Ѕ![]() £љ144£ї
£љ144£ї
≤є»ЂЌЉ–ќ»зѕ¬£Ї
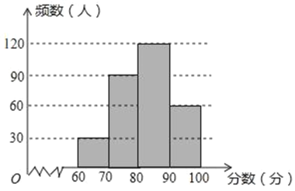 °≠
°≠
£®2£©µЏ150Єц эЊЁЇЌµЏ151Єц эЊЁ‘ЏC„й£ђЋщ“‘ эЊЁµƒ÷–ќї э‘ЏC„й£ђ
Ћщ“‘Ћыµƒ≥…Љ®‘ЏC„й
є ір∞Єќ™144£ђC£ї
£®3£©Ѕ–±н»зѕ¬£Ї
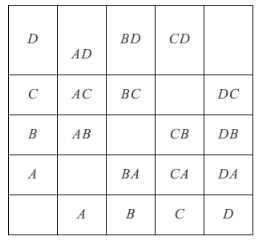
”…±нњ…÷™є≤”–12÷÷µ»њ…ƒ№љбєы£ђ≥йµљA°ҐC„й»Ћµƒє≤”–Ѕљ÷÷љбєы£ђ
°аP£®AC£©£љ![]() £љ
£љ![]() £Ѓ
£Ѓ
£®4£©18000°Ѕ£®![]() £©=1080
£©=1080