ЬтФПФкШн
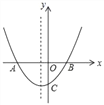
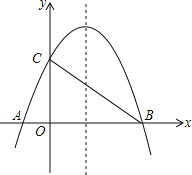
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=Љ![]() +bx+4гыxжсЯрНЛгкAЁЂBСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌШєвбжЊBЕуЕФзјБъЮЊBЃЈ8ЃЌ0ЃЉЃЎ
+bx+4гыxжсЯрНЛгкAЁЂBСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌШєвбжЊBЕуЕФзјБъЮЊBЃЈ8ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЦфЖдГЦжсЗНГЬЃЛ
ЃЈ2ЃЉСЌНгACЁЂBCЃЌЪдХаЖЯЁїAOCгыЁїCOBЪЧЗёЯрЫЦЃПВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉMЮЊХзЮяЯпЩЯBCжЎМфЕФвЛЕуЃЌNЮЊЯпЖЮBCЩЯЕФвЛЕуЃЌШєMNЁЮyжсЃЌЧѓMNЕФзюДѓжЕЃЛ
ЃЈ4ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЁїACQЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіЗћКЯЬѕМўЕФQЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌЖдГЦжсЃК
ЃЌЖдГЦжсЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЯрЫЦЃЌРэгЩМћЪдЬтНтЮіЃЛ
ЃЈ3ЃЉ4ЃЛ
ЃЈ4ЃЉQ1ЃЈ3ЃЌ0ЃЉЃЌQ2ЃЈ3ЃЌ![]() ЃЉЃЉЃЌQ3ЃЈ3ЃЌ
ЃЉЃЉЃЌQ3ЃЈ3ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉАбЕуBЕФзјБъДњШыХзЮяЯпНтЮіЪНЧѓГіbЕФжЕЃЌМДПЩЕУЕНХзЮяЯпНтЮіЪНЃЌдйИљОнЖдГЦжсЗНГЬСаЪНМЦЫуМДПЩЕУНтЃЛ
ЃЈ2ЃЉСюy=0ЃЌНтЗНГЬЧѓГіЕуAЕФзјБъЃЌСюx=0ЧѓГіyЕФжЕЕУЕНЕуCЕФзјБъЃЌдйЧѓГіOAЁЂOBЁЂOCЃЌШЛКѓИљОнЖдгІБпГЩБШР§ЃЌМаНЧЯрЕШЕФСНИіШ§НЧаЮЯрЫЦжЄУїЃЛ
ЃЈ3ЃЉЩшжБЯпBCЕФНтЮіЪНЮЊ![]() ЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіНтЮіЪНЃЌдйБэЪОГіMNЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФзюжЕЮЪЬтНтД№ЃЛ
ЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіНтЮіЪНЃЌдйБэЪОГіMNЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФзюжЕЮЪЬтНтД№ЃЛ
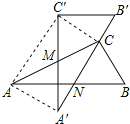
ЃЈ4ЃЉРћгУЙДЙЩЖЈРэСаЪНЧѓГіACЃЌЙ§ЕуCзїCDЁЭЖдГЦжсгкDЃЌШЛКѓЗжЂйAC=CQЪБЃЌРћгУЙДЙЩЖЈРэСаЪНЧѓГіDQЃЌЗжЕуQдкЕуDЕФЩЯЗНКЭЯТЗНСНжжЧщПіЧѓГіЕуQЕНxжсЕФОрРыЃЌдйаДГіЕуЕФзјБъМДПЩЃЛЂкЕуQЮЊЖдГЦжсгыxжсЕФНЛЕуЪБЃЌAQ=CQЃЌдйаДГіЕуQЕФзјБъМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпЕуBЃЈ8ЃЌ0ЃЉдкХзЮяЯп![]() ЩЯЃЌЁр
ЩЯЃЌЁр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊ
ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп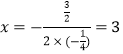 ЃЛ
ЃЛ
ЃЈ2ЃЉЁїAOCЁзЁїCOBЃЎРэгЩШчЯТЃКСюy=0ЃЌдђ![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЁрЕуAЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌСюx=0ЃЌдђy=4ЃЌЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ4ЃЉЃЌЁрOA=2ЃЌOB=8ЃЌOC=4ЃЌЁп
ЃЌЁрЕуAЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌСюx=0ЃЌдђy=4ЃЌЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ4ЃЉЃЌЁрOA=2ЃЌOB=8ЃЌOC=4ЃЌЁп![]() =2ЃЌЁЯAOC=ЁЯCOB=90ЁуЃЌЁрЁїAOCЁзЁїCOBЃЛ
=2ЃЌЁЯAOC=ЁЯCOB=90ЁуЃЌЁрЁїAOCЁзЁїCOBЃЛ
ЃЈ3ЃЉЩшжБЯпBCЕФНтЮіЪНЮЊ![]() ЃЌдђЃК
ЃЌдђЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК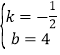 ЃЌЁржБЯпBCЕФНтЮіЪНЮЊ
ЃЌЁржБЯпBCЕФНтЮіЪНЮЊ![]() ЃЌЁпMNЁЮyжсЃЌЁрMN=
ЃЌЁпMNЁЮyжсЃЌЁрMN=![]() =
=![]() =
=![]() ЃЌЁрЕБx=4ЪБЃЌMNЕФжЕзюДѓЃЌзюДѓжЕЮЊ4ЃЛ
ЃЌЁрЕБx=4ЪБЃЌMNЕФжЕзюДѓЃЌзюДѓжЕЮЊ4ЃЛ
ЃЈ4ЃЉгЩЙДЙЩЖЈРэЕУЃЌAC=![]() ЃЌЙ§ЕуCзїCDЁЭЖдГЦжсгкDЃЌдђCD=3ЃЌЂйAC=CQЪБЃЌDQ=
ЃЌЙ§ЕуCзїCDЁЭЖдГЦжсгкDЃЌдђCD=3ЃЌЂйAC=CQЪБЃЌDQ=![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЕуQдкЕуDЕФЩЯЗНЪБЃЌЕуQЕНxжсЕФОрРыЮЊ![]() ЃЌДЫЪБЕуQ1ЃЈ3ЃЌ
ЃЌДЫЪБЕуQ1ЃЈ3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЕуQдкЕуDЕФЯТЗНЪБЃЌЕуQЕНxжсЕФОрРыЮЊ![]() ЃЌДЫЪБЕуQ2ЃЈ3ЃЌ
ЃЌДЫЪБЕуQ2ЃЈ3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЂкЕуQЮЊЖдГЦжсгыxжсЕФНЛЕуЪБЃЌAQ=5ЃЌCQ=![]() =5ЃЌЁрAQ=CQЃЌДЫЪБЃЌЕуQ3ЃЈ3ЃЌ0ЃЉЃЌ
=5ЃЌЁрAQ=CQЃЌДЫЪБЃЌЕуQ3ЃЈ3ЃЌ0ЃЉЃЌ
злЩЯЫљЪіЃЌЕуQЕФзјБъЮЊЃЈ3ЃЌ![]() ЃЉЛђЃЈ3ЃЌ
ЃЉЛђЃЈ3ЃЌ![]() ЃЉЛђЃЈ3ЃЌ0ЃЉЪБЃЌЁїACQЮЊЕШбќШ§НЧаЮЪБЃЎ
ЃЉЛђЃЈ3ЃЌ0ЃЉЪБЃЌЁїACQЮЊЕШбќШ§НЧаЮЪБЃЎ


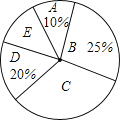
ЁОЬтФПЁПНќФъРДЃЌжабЇЩњЕФЩэЬхЫижЪЦеБщЯТНЕЃЌФГаЃЮЊСЫЬсИпБОаЃбЇЩњЕФЩэЬхЫижЪЃЌТфЪЕНЬг§ВПУХЁАдкаЃбЇЩњУПЬьЬхг§ЖЭСЖЪБМфВЛЩйгк1аЁЪБЁБЕФЮФМўОЋЩёЃЌЖдВПЗжбЇЩњЕФУПЬьЬхг§ЖЭСЖЪБМфНјааСЫЕїВщЭГМЦЃЎвдЯТЪЧБОДЮЕїВщНсЙћЕФЭГМЦБэКЭЭГМЦЭМЃЎ
зщБ№ | A | B | C | D | E |
ЪБМфtЃЈЗжжгЃЉ | tЃМ40 | 40ЁмtЃМ60 | 60ЁмtЃМ80 | 80ЁмtЃМ100 | tЁн100 |
ШЫЪ§ | 12 | 30 | a | 24 | 12 |
ЃЈ1ЃЉЧѓГіБОДЮБЛЕїВщЕФбЇЩњЪ§ЃЛ
ЃЈ2ЃЉЧыЧѓГіЭГМЦБэжаaЕФжЕЃЛ
ЃЈ3ЃЉЧѓИїзщШЫЪ§ЕФжкЪ§ЃЛ
ЃЈ4ЃЉИљОнЕїВщНсЙћЃЌЧыФуЙРМЦИУаЃ2400УћбЇЩњжаУПЬьЬхг§ЖЭСЖЪБМфВЛЩйгк1аЁЪБЕФбЇЩњШЫЪ§ЃЎ