Question

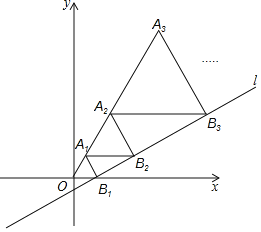
【题目】如图，在平面直角坐标系xOy中，直线l：y=x-与x轴交于点B1，以OB1为边长作等边三角形A1OB1，过点A1作A1B2平行于x轴，交直线l于点B2，以A1B2为边长作等边三角形A2A1B2，过点A2作A2B3平行于x轴，交直线l于点B3，以A2B3为边长作等边三角形A3A2B3，…，按此规律进行下去，则点A3的横坐标为______；点A2018的横坐标为______．

Answer 1

【答案】

【解析】

利用一次函数图象上点的坐标特征可求出点B1的坐标，根据等边三角形的性质可求出点A1的坐标，同理可得出点B2、A2、A3的坐标，根据点An坐标的变化即可得出结论．

当y=0时，有x-=0，

解得：x=1，

∴点B1的坐标为（1，0），

∵A1OB1为等边三角形，

∴点A1的坐标为（，）．

当y=时．有x-=，

解得：x=，

∴点B2的坐标为（，），

∵A2A1B2为等边三角形，

∴点A2的坐标为（，）．

同理，可求出点A3的坐标为（，），点A2018的坐标为（，）．

故答案为：；．