题目内容
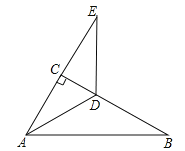
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
【答案】30°;见解析.
【解析】
试题分析:根据∠ACB和∠B的度数得出∠CAB的度数,根据角平分线的性质得出∠CAD的度数;根据∠ACD+∠ECD=180°,∠ACD=90°得出∠ACD=∠ECD=90°,证明△ACD和△ECD全等,从而得出结论.
试题解析:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°, ∴∠CAB=60°.
又∵AD平分∠CAB, ∴∠CAD=![]() ∠CAB=30°,即∠CAD=30°;
∠CAB=30°,即∠CAD=30°;
(2)证明:∵∠ACD+∠ECD=180°,且∠ACD=90°, ∴∠ECD=90°, ∴∠ACD=∠ECD.
在△ACD与△ECD中,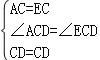 , ∴△ACD≌△ECD(SAS), ∴DA=DE.
, ∴△ACD≌△ECD(SAS), ∴DA=DE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目