题目内容
【题目】如图,AC平分∠BAD,CD⊥AD,CB⊥AB,连结BD.请找出图中所有的等腰三角形,并说明理由.
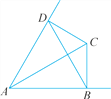
【答案】等腰三角形有△ABD和△BCD
【解析】试题分析:本题先利用角平分线的性质可证CD=CB,再根据HL判定△ADC≌△ADC,根据AC平分∠BAD,CD⊥AD,CB⊥AB,可证CD=CB,所以△CDB是等腰三角形.在Rt△ADC和Rt△ABC中,由CD=CB,AC=AC,可判定Rt△ADC≌Rt△ABC,从而可得AD=AB,所以△ABD是等腰三角形.
试题解析:等腰三角形有△ABD和△BCD,
理由如下:
∵ AC平分∠BAD,CD⊥ AD,CB⊥ AB,
∴ CD=CB,
∴ △CDB是等腰三角形,
在Rt△ADC和Rt△ABC中,
![]() ,
,
∴ Rt△ADC≌Rt△ABC(HL),
∴ AD=AB,
∴ △ ABD是等腰三角形.
点睛:本题要考查角平分线的性质,HL判定定理,等腰三角形的判定,解决本题的关键在于熟练掌握角平分线的性质,利用角平分线上的点到角两边的距离相等证明线段相等,再利用HL进行全等判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目