题目内容
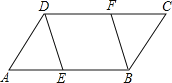
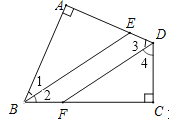
【题目】把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
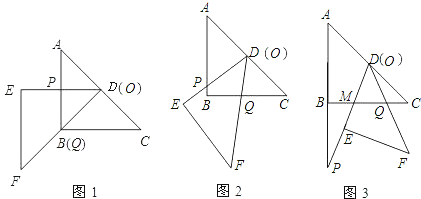
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,APCQ= ;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问APCQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
【答案】(1)8.(2)APCQ的值不会改变.(3)当2<x<4时,y=8﹣x﹣![]() .当0<x≤2时,y=4﹣x﹣
.当0<x≤2时,y=4﹣x﹣![]() (或y=
(或y=![]() ).
).
【解析】
试题分析:(1)可通过证△APD∽△CDQ来求解.
(2)不会改变,关键是还是证△APD∽△CDQ,已知了一组45°角,关键是证(1)中的∠APD=∠QDC,由于图2由图1旋转而得,根据旋转的性质可设旋转角为α,那么∠APD=90°﹣α,∠CDQ=90°﹣α,因此两角相等.由此可证得两三角形相似.因此结论不变.
(3)本题分类两种情况进行讨论:①当0°<α<45°时②当45°≤α<90°时.
解:(1)∵∠A=∠C=45°,∠APD=∠QDC=90°,
∴△APD∽△CDQ.
∴AP:CD=AD:CQ.
∴即AP×CQ=AD×CD,
∵AB=BC=4,
∴斜边中点为O,
∴AP=PD=2,
∴AP×CQ=2×4=8;
故答案为:8.
(2)APCQ的值不会改变.
理由如下:
∵在△APD与△CDQ中,∠A=∠C=45°,
∠APD=180°﹣45°﹣(45°+α)=90°﹣α,
∠CDQ=90°﹣α,
∴∠APD=∠CDQ.
∴△APD∽△CDQ.
∴![]() .
.
∴APCQ=ADCD=AD2=(![]() AC)2=8.
AC)2=8.
(3)情形1:当0°<α<45°时,2<CQ<4,即2<x<4,
此时两三角板重叠部分为四边形DPBQ,过D作DG⊥AP于G,DN⊥BC于N,
∴DG=DN=2
由(2)知:APCQ=8得AP=![]()
于是y=![]() ABBC﹣
ABBC﹣![]() CQDN﹣
CQDN﹣![]() APDG
APDG
=8﹣x﹣![]() (2<x<4)
(2<x<4)
情形2:当45°≤α<90°时,0<CQ≤2时,即0<x≤2,此时两三角板重叠部分为△DMQ,
由于AP=![]() ,PB=
,PB=![]() ﹣4,易证:△PBM∽△DNM,
﹣4,易证:△PBM∽△DNM,
∴![]() 即
即![]() 解得
解得![]() .
.
∴MQ=4﹣BM﹣CQ=4﹣x﹣![]() .
.
于是y=![]() MQDN=4﹣x﹣
MQDN=4﹣x﹣![]() (0<x≤2).
(0<x≤2).
综上所述,当2<x<4时,y=8﹣x﹣![]() .
.
当0<x≤2时,y=4﹣x﹣![]() (或y=
(或y=![]() ).
).