��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l���ڵ�ֱ�ߵĽ���ʽΪy=![]() x����B����Ϊ��10��0����B��BC��ֱ��l������ΪC����P��ԭ�������x�᷽�����B�˶����ٶ�Ϊ1��λ/s��ͬʱ��Q�ӵ�B������B��C��ԭ�㷽���˶����ٶ�Ϊ2����λ/s����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶���
x����B����Ϊ��10��0����B��BC��ֱ��l������ΪC����P��ԭ�������x�᷽�����B�˶����ٶ�Ϊ1��λ/s��ͬʱ��Q�ӵ�B������B��C��ԭ�㷽���˶����ٶ�Ϊ2����λ/s����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶���
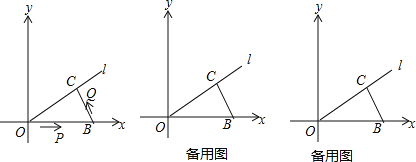
��1��OC= ��BC= ��
��2����t=5��s��ʱ������ֱ��PQ��ȷ��һ��M��ʹ��BCM���ܳ���С�����������Сֵ��
��3�����P���˶�ʱ��Ϊt��s������PBQ�����Ϊy������PBQ����ʱ����y��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
���𰸡���1��8��6����2��16����3��y= ��
��
��������
�����������1�����ݹ��ɶ������ɵô𰸣�
��2�������߶δ�ֱƽ���ߵ����ʣ��ɵ�ֱ��PQ�ϵĵ㵽O��C�ľ�����ȣ���������֮���߶���̣��ɵ�M����P���غϣ����������ε��ܳ����ɵô𰸣�
��3�������ٶ���ʱ��Ĺ�ϵ���ɵ�OP��BQ���������к������ɵ�QH�����������ε������ʽ���ɵô𰸣�
�⣺��1����ֱ��l���ڵ�ֱ�ߵĽ���ʽΪy=![]() x��BC��ֱ��l��
x��BC��ֱ��l��
��![]() =
=![]() ��
��
����OB=10��BC=3x��OC=4x��
����3x��2+��4x��2=102��
���x=2��x=��2���ᣩ��
OC=4x=8��BC=3x=6��
�ʴ�Ϊ��8��6��
��2����ͼ1��
 ��
��
PQ��OC�Ĵ�ֱƽ���ߣ�OB��PQ��P��M����P���غϣ�
M��P���غ�ʱ��BCM���ܳ���С��
�ܳ���СΪ=BM+PM+BC=OB+BC=10+6=16��
��3���ٵ�0��t��3ʱ����Q��QH��OB����ΪH����ͼ2��
 ��
��
PB=10��t��BQ=2t��HQ=2tsinB=2tcos��COB=2t��![]() =
=![]() t��
t��
y=![]() PBQH=
PBQH=![]() ��10��t��
��10��t��![]() t=��
t=��![]() t2+8t��
t2+8t��
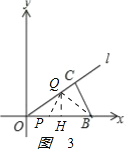
�ڵ�3��t��5ʱ����Q��QH��OB����ΪH����ͼ3��
 ��
��
PB=10��t��OQ=OC+BC��2t=14��2t��
QH=OQsin��QOH=��14��2t��![]() =
=![]() ��14��2t��=
��14��2t��=![]() ��
��![]() t��
t��
y=![]() PBQH=
PBQH=![]() ��10��t����
��10��t����![]() ��
��![]() t��=
t��=![]() t2��
t2��![]() t+42��
t+42��
��������y= ��
��