题目内容
如图，一根5米长的绳子一端系在墙角O处，另一端系着一只小羊，已知OA=AB=4米，BC=1米，OD=DE=EF=3米，请画出小羊可活动的区域并求出该区域的面积（结果保留π）．
分析：结合图形，发现：小羊在草地上的最大活动区域的面积=圆心角是90°，半径是5的扇形面积+圆心角是90°，半径是1米和2米的扇形面积，求出即可．
解答：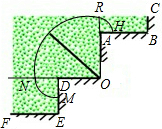
解：小羊在草地上的最大活动区域如图所示，
∵扇形ARH的半径为5-4=1米，扇形CDM的半径为5-3=2米，
∴小羊在草地上的最大活动区域的面积，
=S扇形ARH+S扇形NDM+S扇形NOR，
=
+
+
=
π．
解：小羊在草地上的最大活动区域如图所示，∵扇形ARH的半径为5-4=1米，扇形CDM的半径为5-3=2米，
∴小羊在草地上的最大活动区域的面积，
=S扇形ARH+S扇形NDM+S扇形NOR，
=
| 90π×52 |
| 360 |
| 90π×1 2 |
| 360 |
| 90×π×2 2 |
| 360 |
| 15 |
| 2 |
点评：此题主要考查了扇形面积公式应用，此题要注意墙角的木桩的阻碍，导致小羊在草地上的最大活动区域的面积应分为三部分进行计算．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
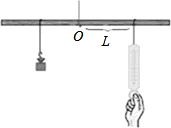如图，取一根长1米长的匀质木杆，用细绳绑在木杆的中点O处并将其吊起来，在中点的左侧距离中点25cm处挂一个重9.8牛顿的物体，在中点右侧用一个弹簧秤向下拉，改变弹簧称与中点O的距离L（单位：cm），看弹簧秤的示数F（单位：牛顿）有什么变化，小明在做此《数学活动》时，得到下表的数据：| L/cm | 1 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| F/牛顿 | 125 | 24.5 | 16.5 | 12.3 | 9.8 | 8.2 | 7 | █ | 5.4 |
（1）当L=
（2）被墨水涂黑了的数据你认为大概是
（3）你能求出F与L的函数关系式吗？
（4）请你在直角坐标系中画出此函数的图象．
≈1.8，
≈1.9，
≈2.1)．
如图取一根长1.2米的匀质木杆，用细绳绑在木杆的中点O处并将其吊起来．
在左侧距离中点30cm处挂一个重10N的物体，为了保持木杆水平，在右侧用一个弹簧秤竖直向下拉．改变弹簧称与中点O的距离（单位：cm），看弹簧秤的示数F（单位：N）有什么变化，小锐在做此活动时，得到下表的数据：
| l/cm | … | 10 | 15 | 20 | 25 | b | … |
| F/N | … | 30 | 20 | a | 12 | 10 | … |
（2）求F与l的函数解析式；
（3）在平面直角坐标系中画出此函数的图象．
如图，取一根长1米长的匀质木杆，用细绳绑在木杆的中点O处并将其吊起来，在中点的左侧距离中点25cm处挂一个重9.8牛顿的物体，在中点右侧用一个弹簧秤向下拉，改变弹簧称与中点O的距离L（单位：cm），看弹簧秤的示数F（单位：牛顿）有什么变化，小明在做此《数学活动》时，得到下表的数据：
| L/cm | 1 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| F/牛顿 | 125 | 24.5 | 16.5 | 12.3 | 9.8 | 8.2 | 7 | █ | 5.4 |
（1）当L=______cm时的数据是错了；
（2）被墨水涂黑了的数据你认为大概是______；
（3）你能求出F与L的函数关系式吗？
（4）请你在直角坐标系中画出此函数的图象．