��Ŀ����
����Ŀ�� ���һ���������ܱ�ʾΪ��������������ƽ�����ô���dz����������Ϊ����г��������8=32-12��16=52-32��24=72-52����ˣ�8��16��24����������������г������
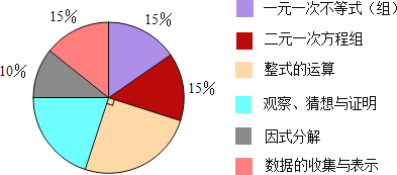
��1����32��75��80���������У��Ǻ�г������______��
��2����200Ϊ��г������200����д����������������ƽ��������������������ĺ�Ϊ______��
��3��С��ͨ���۲췢���������������г������Ϊ8�ı�������������������Ϊ2n-1��2n+1������nȡ��������������ͨ��������֤����г����8�ı�������������Ƿ���ȷ��
���𰸡���1��32��80����2��100����3������г����8�ı����������������ȷ�ģ�֤���������
��������
��1�����ݡ���г�����Ķ��壬���һ������������г��Ӧ����ʲô�������Դ������ж�32��75��80���������У���Щ���Ǻ�г����
��2������ĸ��ʾ���������������г�����ɺ�г����200���г����̣�������õ��������������������Ӷ�����������������������ĺͣ�
��3������ĸ��ʾ���������������г����ͨ��������֤�����۳�����
�⣺��1���ɡ���г�����Ķ��壬�������������������ֱ�Ϊ![]() ��
��![]() ��
��
���г���ɱ�ʾΪ��![]() ��������
��������![]() ��ʾ��������
��ʾ��������
�ࡰ��г��������8������������
��32��80����г����75���Ǻ�г������32=92-72��80=212-192��
�ʴ�Ϊ��32��80.
��2����![]() 200����
200����![]() 200��
200��
��![]() ��
��
��![]() ��
��![]() ��
��
��49+51=100��
�����������������ĺ�Ϊ100��
�ʴ�Ϊ��100.
��3��֤������![]() ,
,
�ࡰ��г����8�ı����������������ȷ�ģ�