Question

【题目】如图，一次函数y=﹣2x+4与x轴，y轴分别交于A，B，以线段AB为直角边在第一象限内作Rt△ABC，使AB=AC．

（1）求直线AC的函数关系式；

（2）若P（m，3）在第二象限内，求当△PAB与△ABC面积相等时m的值．

Answer 1

【答案】（1）y=x﹣1；（2）m=﹣．

【解析】

（1）过点C作CD⊥x轴于点D，利用△ABO≌△CAD，求出点C的坐标，最后利用待定系数法求出AC的解析式．

（2）过点P作PE⊥x轴于点E，利用勾股定理即可求出AB=AC=2，利用S△APB=SOAB+S△OPB﹣S△OPA列出方程求出m的值．

（1）令x=0代入y=﹣2x+4中

∴y=4，

∴B（0，4）

令y=0代入y=﹣2x+4中

∴x=2，

∴A（2，0）

过点C作CD⊥x轴于点D，

∵∠BAC=90°，

∴∠DAC+∠BAO= +∠BAO=90°，

∴∠ABO=∠DAC，

在△ABO与△CAD中，

∴△ABO≌△CAD（AAS）

∴C∠ABO D=OA=2，AD=OB=4，

∴OD=6，

∴C（6，2）

设直线AC的解析式为y=kx+b

∴

∴解得：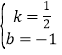

∴直线AC的解析式为：y=x﹣1

（2）过点P作PE⊥x轴于点E，

∴PE=3，OE=﹣m

∵AB=AC=2

∴S△ABC=ACAB=×2×2=10

∴S△APB=SOAB+S△OPB﹣S△OPA

=AOBO+OBOE﹣OAPE

=1﹣2m

∴1﹣2m=10

∴m=﹣ ．