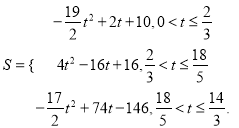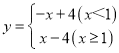题目内容
【题目】如图,在△ABC中,tan∠ABC=![]() ,∠ACB=45°,AD=8,AD是边BC上的高,垂足为D,BE=4,点M从点B出发沿BC方向以每秒3个单位的速度运动,点N从点E出发,与点M同时同方向以每秒1个单位的速度运动.以MN为边在BC的上方作正方形MNGH.点M到达点C时停止运动,点N也随之停止运动.设运动时间为t(秒)(t>0).
,∠ACB=45°,AD=8,AD是边BC上的高,垂足为D,BE=4,点M从点B出发沿BC方向以每秒3个单位的速度运动,点N从点E出发,与点M同时同方向以每秒1个单位的速度运动.以MN为边在BC的上方作正方形MNGH.点M到达点C时停止运动,点N也随之停止运动.设运动时间为t(秒)(t>0).
(1)当t为多少秒时,点H刚好落在线段AB上?
(2)当t为多少秒时,点H刚好落在线段AC上?
(3)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,求出S关于t的函数关系式并写出自变量t的取值范围.

【答案】(1)当t为![]() 秒时,点H刚好落在线段AB上;(2)当t为
秒时,点H刚好落在线段AB上;(2)当t为![]() 秒时,点H刚好落在线段AC上; (3)S关于t的函数关系式为:S=
秒时,点H刚好落在线段AC上; (3)S关于t的函数关系式为:S=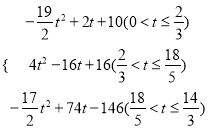 .
.
【解析】分析: ![]() 如图1中,当H在AB上时,易知
如图1中,当H在AB上时,易知![]() 根据
根据![]() 列出方程即可解决问题;
列出方程即可解决问题;
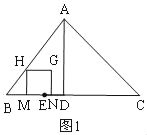
![]() 如图2中,当H在AC上时,根据
如图2中,当H在AC上时,根据![]() 列出方程即可解决问题;
列出方程即可解决问题;
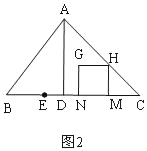
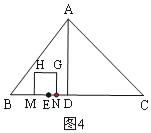
![]() 分四种情形列出方程即可①如图3中,当
分四种情形列出方程即可①如图3中,当![]() 时,重叠部分是五边形MNGPK.②如图4中,当
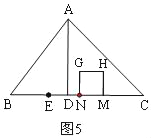
时,重叠部分是五边形MNGPK.②如图4中,当![]() 时,重叠部分是正方形MNGH.③如图5中,当
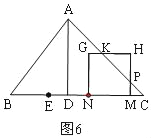
时,重叠部分是正方形MNGH.③如图5中,当![]() 时,重叠部分是四边形MNGH.④如图6中,当
时,重叠部分是四边形MNGH.④如图6中,当![]() 时,重叠部分是五边形MNGKP;
时,重叠部分是五边形MNGKP;
详解:(1)如图1,当H在AB上时,
在Rt ![]() 中,
中, ![]()
∴BD=6,
在Rt ![]() 中,∵
中,∵![]()
![]()
由题意得: ![]()
∴![]()
∵四边形MNGH是正方形,
∴![]()
即![]()
当t为![]() 秒时,点H刚好落在线段AB上;
秒时,点H刚好落在线段AB上;
(2)如图2,H在AC上时,
由题意得: ![]() 则
则![]()
![]()
∵![]()
∴![]()
![]()
当t为![]() 秒时,点H刚好落在线段AC上;
秒时,点H刚好落在线段AC上;
(3)分四种情况:
①如图3,当![]() 时,重叠部分是五边形MNGPK,
时,重叠部分是五边形MNGPK,
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
![]()
∴S=S正方形MNGH-S△PHK,
![]()
![]()
![]()
②如图4,当![]() 时,重叠部分为正方形MNGH,
时,重叠部分为正方形MNGH,
∴![]()
③如图5,当![]() 时,重叠部分为正方形MNGH,
时,重叠部分为正方形MNGH,
∴![]()
④如图6,当![]() 时,重叠部分为五边形GNMPK,
时,重叠部分为五边形GNMPK,
∵![]() ,
,
∴![]()
∵![]()
同理可得:S=S正方形MNGH-S△PHK,
![]()
![]()
![]()
综上所述,S关于t的函数关系式为: