题目内容
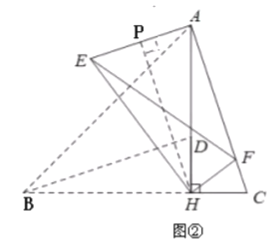
【题目】如图①,△ABC中,∠ABC=45°,AH⊥BC 于H,点D在AH上,且DH=CH,连结BD.将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.如图②,当点F落在AC上时(F不与C重合),若BC=4,tan∠ACH=3,则AE=_____.

【答案】![]()
![]()
![]()
![]()
【解析】在Rt△AHC中,由tan∠ACH=3,可得![]() =3, 设CH=x,则BH=AH=3x,由BC=4, 可得 3x+x=4, 解得 x=1.即可得AH=3, CH=1. 由旋转知:∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH. 所以∠EHA=∠FHC,
=3, 设CH=x,则BH=AH=3x,由BC=4, 可得 3x+x=4, 解得 x=1.即可得AH=3, CH=1. 由旋转知:∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH. 所以∠EHA=∠FHC, ![]() =1,即可判定△EHA∽△FHC,所以∠EAH=∠C,即可得tan∠EAH=tanC=3 ,如图②,过点H作HP⊥AE于P,则HP=3AP,AE=2AP. 在Rt△AHP中,AP2+HP2= AH2,∴AP2+(3AP)2= 9,解得AP=
=1,即可判定△EHA∽△FHC,所以∠EAH=∠C,即可得tan∠EAH=tanC=3 ,如图②,过点H作HP⊥AE于P,则HP=3AP,AE=2AP. 在Rt△AHP中,AP2+HP2= AH2,∴AP2+(3AP)2= 9,解得AP=![]() ,所以AE=
,所以AE=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





