��Ŀ����
����{a��b��c}Ϊ����y=ax2+bx+c�ġ������������磺����y=x2-2x+3�ġ�����������{1��-2��3}������y=2x+3�ġ�����������{0��2��3}������y=-x�ġ�����������{0��-1��0}��1����������������
 �ĺ���ͼ������ƽ��2����λ���õ�һ���º���������º����Ľ���ʽ��y=
�ĺ���ͼ������ƽ��2����λ���õ�һ���º���������º����Ľ���ʽ��y= ��
����2���ڣ�1���У�ƽ��ǰ������������ֱ���y�ύ��A��B���㣬��ֱ��x=
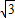 �ֱ���D��C���㣬�ж���A��B��C��D�ĵ�Ϊ������ı�����״����˵�����ɲ��������ܳ���
�ֱ���D��C���㣬�ж���A��B��C��D�ĵ�Ϊ������ı�����״����˵�����ɲ��������ܳ�����3������2���е��ı����롰����������
 �ĺ���ͼ����н��㣬������������ʵ��b��ȡֵ��Χ��
�ĺ���ͼ����н��㣬������������ʵ��b��ȡֵ��Χ��
���𰸡���������1�����ݺ�������������д�������Ľ���ʽ���ٸ���ƽ�ƺ�һ�κ����ı仯���д������ͼ������ƽ��2����λ���º����Ľ���ʽ��
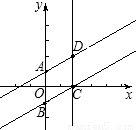
��2���ж���A��B��C��D�ĵ�Ϊ������ı�����״���ɸ���һ�κ���ͼ������ƽ��2����λ��ԭ����ͼ��Ĺ�ϵ���ó�AB=2����ȷ��Ϊƽ���ı��Σ���ֱ���ཻ���㽻�����������߶�BC=2���ٸ������ε��ж����ڱ���ȵ�ƽ���ı��������Σ��ó������ܳ�=2×4=8��
��3�����ݺ�������������д�����κ����Ľ���ʽ����Ϊ����ʽΪy=��x-b��2+ ��ȷ�����κ�����ͼ�ᾭ����B�͵�C���ٽ����ζ���A��0��1����D��
��ȷ�����κ�����ͼ�ᾭ����B�͵�C���ٽ����ζ���A��0��1����D��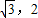 ��������κ�������ʽ�ó�ʵ��b��ȡֵ��Χ��
��������κ�������ʽ�ó�ʵ��b��ȡֵ��Χ��
����⣺��1��y=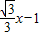 ��1�֣�������������
��1�֣�������������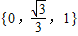 �ĺ�����
�����
��y=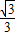 +1��
+1��
�ú���ͼ������ƽ��2����λ����y=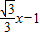 ��
��
��2���������֪y=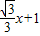 ����ƽ��������λ��y=
����ƽ��������λ��y=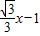
��AD��BC��AB=2��
��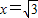 ��
��
��AB��CD��
���ı���ABCDΪƽ���ı��Σ�
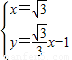 ��
��
��C��������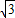 ��0����
��0����
��D��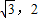 ��
��
�ɹ��ɶ����ɵ�BC=2
���ı���ABCDΪƽ���ı��Σ�AB=2��BC=2
���ı���ABCDΪ���Σ�
���ܳ�Ϊ8��
��3�����κ���Ϊ��y=x2-2bx+b2+ ����Ϊ����ʽΪ��y=��x-b��2+
����Ϊ����ʽΪ��y=��x-b��2+ ��
��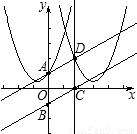
����κ�����ͼ�ᾭ����B�͵�C��
����κ�����ͼ�����ı����й������֣�
�����κ�����ͼ����Aʱ����A��0��1����������κ�����
���b=-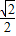 ��b=
��b=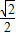 ���������⣬��ȥ����
���������⣬��ȥ����
�����κ�����ͼ����Dʱ��
��D��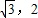 ��������������
��������������
���b=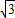 +
+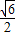 ��b=
��b=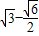 ���������⣬��ȥ����
���������⣬��ȥ����
����ʵ��b��ȡֵ��Χ��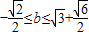 ��
��
�����������ϡ����������Ķ��忼��һ�κ��������κ������ۺ�Ӧ�ã��ۺ���ǿ������Ҫ��ߣ�
��2���ж���A��B��C��D�ĵ�Ϊ������ı�����״���ɸ���һ�κ���ͼ������ƽ��2����λ��ԭ����ͼ��Ĺ�ϵ���ó�AB=2����ȷ��Ϊƽ���ı��Σ���ֱ���ཻ���㽻�����������߶�BC=2���ٸ������ε��ж����ڱ���ȵ�ƽ���ı��������Σ��ó������ܳ�=2×4=8��
��3�����ݺ�������������д�����κ����Ľ���ʽ����Ϊ����ʽΪy=��x-b��2+
 ��ȷ�����κ�����ͼ�ᾭ����B�͵�C���ٽ����ζ���A��0��1����D��
��ȷ�����κ�����ͼ�ᾭ����B�͵�C���ٽ����ζ���A��0��1����D��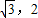 ��������κ�������ʽ�ó�ʵ��b��ȡֵ��Χ��
��������κ�������ʽ�ó�ʵ��b��ȡֵ��Χ������⣺��1��y=
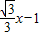 ��1�֣�������������
��1�֣�������������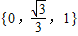 �ĺ�����
�������y=
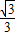 +1��
+1���ú���ͼ������ƽ��2����λ����y=
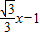 ��
��
��2���������֪y=
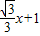 ����ƽ��������λ��y=
����ƽ��������λ��y=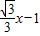
��AD��BC��AB=2��
��
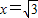 ��
����AB��CD��
���ı���ABCDΪƽ���ı��Σ�
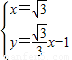 ��
����C��������
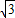 ��0����
��0������D��
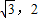 ��
���ɹ��ɶ����ɵ�BC=2
���ı���ABCDΪƽ���ı��Σ�AB=2��BC=2
���ı���ABCDΪ���Σ�
���ܳ�Ϊ8��
��3���������y=x2-2bx+b2+
 ����Ϊ����ʽΪ��y=��x-b��2+
����Ϊ����ʽΪ��y=��x-b��2+ ��
��
����κ�����ͼ�ᾭ����B�͵�C��
����κ�����ͼ�����ı����й������֣�
�����κ�����ͼ����Aʱ����A��0��1����������κ�����
���b=-
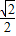 ��b=
��b=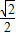 ���������⣬��ȥ����
���������⣬��ȥ���������κ�����ͼ����Dʱ��
��D��
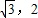 ��������������
�����������������b=
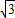 +
+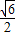 ��b=
��b=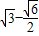 ���������⣬��ȥ����
���������⣬��ȥ��������ʵ��b��ȡֵ��Χ��
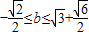 ��
�������������ϡ����������Ķ��忼��һ�κ��������κ������ۺ�Ӧ�ã��ۺ���ǿ������Ҫ��ߣ�

��ϰ��ϵ�д�
�����Ŀ
 ����{a��b��c}Ϊ����y=ax2+bx+c�ġ������������磺����y=x2-2x+3�ġ�����������{1��-2��3}������y=2x+3�ġ�����������{0��2��3}������y=-x�ġ�����������{0��-1��0}
����{a��b��c}Ϊ����y=ax2+bx+c�ġ������������磺����y=x2-2x+3�ġ�����������{1��-2��3}������y=2x+3�ġ�����������{0��2��3}������y=-x�ġ�����������{0��-1��0}